
Dades estadístiques


En aquest material trobareu una introducció a les possibilitats de l'excel com a full de càlcul estadístic, explicacions dels conceptes estadístics bàsics, la descripció de variables qualitatives i quantitatives, i un conjunt de fitxes resum amb els conceptes clau, taules, representacions gràfiques, les fórmules i exemples.
Unitat introductòria. L’Excel com a full de càlcul estadístic
Dades estadístiques
Unitat introductòria. L’Excel com a full de càlcul estadístic
1. Ús com a calculadora: operadors i fórmules
Els operadors aritmètics principals que utilitzarem són:
| Operador | Significat |
|---|---|
| + (signe més) | Suma |
| - (signe menys) | Resta |
| * (asterisc) | Multiplicació |
| / (barra obliqua) | Divisió |
Una fórmula és una equació situada en una casella del full de càlcul que calcula un nou valor a partir dels valors existents en les caselles del full de càlcul.
Les fórmules poden estar formades per nombres, operadors aritmètics, referències a caselles i equacions ja existents en l’Excel que s’anomenen funcions.
Per activar una fórmula:
-
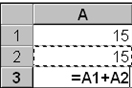
1. Ens situarem en una casella i hi escriurem el signe igual ( = ). Immediatament, apareixerà la barra de fórmules:
 El que escrivim en la casella quedarà reflectit en la barra de fórmules.
El que escrivim en la casella quedarà reflectit en la barra de fórmules.
Alguns exemples de càlcul:
-
2. Una vegada hem escrit la fórmula, cal prémer la tecla “INTRO” i el valor de la fórmula quedarà inserit en la casella.
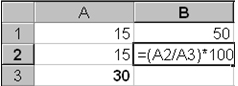
Aquesta opció de l’Excel ens pot ser útil, per exemple, per generar una nova variable a partir de variables que ja tinguem enregistrades.
D'aquesta manera, podríem obtenir la densitat de població d’uns municipis determinats a partir de les dades conegudes de la població i la superfície. Com sabem, obtindrem la densitat de població dividint el nombre d’habitants pels quilòmetres quadrats de superfície del municipi.
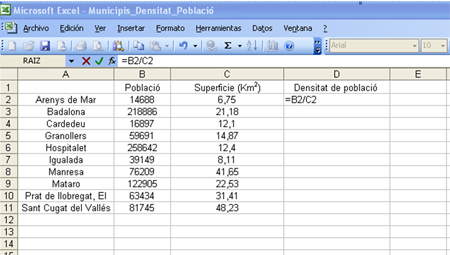
Podem veure l'exemple amb les dades de deu municipis de la província de Barcelona que teniu al fitxer “municipis_densitat_poblacio.xls” (Full 1) :
| Municipi | Població | Superfície (km2) |
|---|---|---|
| Arenys de Mar | 14688 | 6,75 |
| Badalona | 218886 | 21,18 |
| Cardedeu | 16897 | 12,1 |
| Granollers | 59691 | 14,87 |
| Hospitalet | 258642 | 12,4 |
| Igualada | 39149 | 8,11 |
| Manresa | 76209 | 41,65 |
| Mataró | 122905 | 22,53 |
| Prat de Llobregat, El | 63434 | 31,41 |
| Sant Cugat del Vallès | 81745 | 48,23 |
A continuació, us podeu descarregar l’arxiu Excel amb l'exemple sobre densitat de població de la província de Barcelona: Municipis densitat de població
Per obtenir la densitat de població amb l’Excel:
-
1. Ens situarem en la columna lliure següent de les dades de superfície i escriurem el nom de la nova variable en la primera fila («Densitat de població»).
-
2. En la casella següent de la mateixa columna, hi escriurem el signe igual ( = ).
-
3. En la barra de fórmules que apareixerà, hi anotarem la fórmula de càlcul de la densitat del primer municipi d’Arenys de Mar, que serà la «Població» (que tenim a la casella B2), dividit ( / ) per la superfície (casella C2). Podem veure l'exemple en la captura de pantalla següent.
-
4. Quan premem la tecla “INTRO”, el valor de la fórmula quedarà inserit en la casella. Per obtenir els valors de densitat de població de la resta de municipis, només hem d'arrossegar el cursor per la columna fins a l'última fila.
-
Els resultats, sense decimals, són els que es mostren a continuació:

2. Ús de les funcions
Les anàlisis estadístiques es poden mitjançant l’ús del programa com a calculadora, com hem vist anteriorment, o bé utilitzant les anàlisis estadístiques preconfigurades en el full de càlcul.
Així, podem efectuar qualsevol càlcul utilitzant alguna funció predefinida pel programa.
Amb l’Excel, ho podem fer de la manera següent:
-
1. Podem accedir a aquestes funcions mitjançant la seqüència d’instruccions: “INSERTAR” i “FUNCIÓN”.
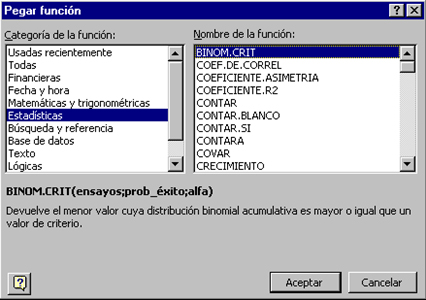
-
2. En la finestra “CATEGORÍA DE LA FUNCIÓN”, seleccionem l’opció “ESTADÍSTICAS” i en el requadre “NOMBRE DE FUNCIÓN”, l’opció de l'indicador que volem obtenir.
Cal tenir en compte que a la casella veurem el resultat de la fórmula, ja que la fórmula la veurem en l’espai d’edició que hi ha a la part superior del full de càlcul.
Quan tractem les diferents anàlisis estadístiques comentarem la funció concreta per a cada indicador.
Podem fer un exemple amb les dades que acabem d'exposar.
Continuem amb l'exemple anterior del fitxer “municipis_densitat_poblacio.xls” (Full 1). Suposem que volem obtenir la mitjana aritmètica (més endavant veurem aquest indicador de tendència central més abastament) del nombre d’habitants («Població»). Vegem a continuació quins passos cal seguir.
La funció de l’Excel que ens calcula la mitjana és la funció “PROMEDIO”:
-
1. Així, ens hem de situar a la primera casella buida de la columna de la variable “Població” (casella B12), i seguir la seqüència d’instruccions: “INSERTAR” i “FUNCIÓN”.
-
2. Tal com hem comentat abans, a la finestra “CATEGORÍA DE LA FUNCIÓN” hem de seleccionar l’opció “ESTADÍSTICAS” i en el requadre “NOMBRE DE FUNCIÓN”, l’opció “PROMEDIO”.
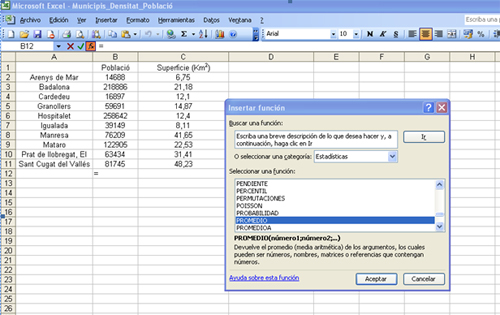
-
3. Si premem “Aceptar”, obtindrem:
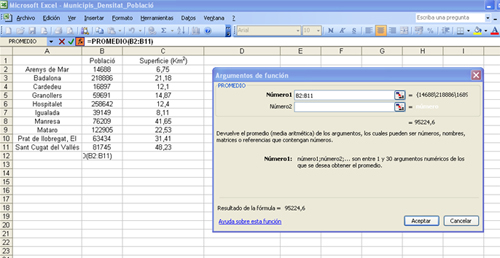
-
4. Com podem veure, l’Excel introdueix el rang de les caselles on hi ha les dades de la variable “Població” (de B2 a B11), i ens proporciona el valor de la mitjana: 95.224,6.
-
5. Si premem “Aceptar”, obtindrem el valor de la mitjana aritmètica a la casella B12.
La mitjana del nombre d’habitants dels deu municipis de la província de Barcelona és de 95.225 (arrodonint a la xifra entera més pròxima).
3. Ús dels programes preconfigurats
L’Excel incorpora una sèrie de programes predefinits que ens permeten dur a terme alguns càlculs estadístics. Per fer-los, el primer que cal fer és activar el mòdul de “ANÁLISIS DE DATOS”. Per activar aquest mòdul cal seguir els passos següents:
-
1. Fer clic en la instrucció “HERRAMIENTAS” de la línia de comandes.
-
2. Fer clic en la comanda “COMPLEMENTOS” del menú desplegat. A continuació, apareixerà una llista dels complements disponibles.
-
3. Dins de la llista, seleccionar la instrucció “HERRAMIENTAS PARA ANÁLISIS”
-
4. Sortir del menú fent clic en la comanda “ACEPTAR”.
Un cop tinguem activats els programes preconfigurats, els passos que hem de seguir per utilitzar-los en el full de càlcul Excel són els següents:
-
1. Fer clic en la comanda “HERRAMIENTAS” del menú principal. A continuació, apareixerà la pantalla següent:
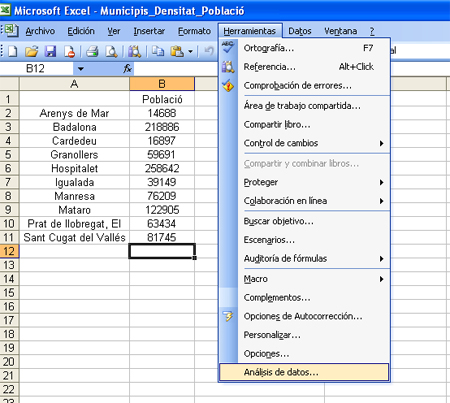
-
2. Fer clic en la instrucció “ANÁLISIS DE DATOS” i s’obrirà el quadre següent:
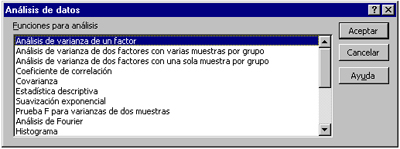
En el quadre es mostren els programes per efectuar diverses anàlisis estadístiques. En les diferents unitats didàctiques, quan tinguem la necessitat de fer servir algun d’aquests programes preconfigurats ja indicarem l’opció que haurem d’activar.
Unitat 1. Conceptes estadístics bàsics
Dades estadístiques
Unitat 1. Conceptes estadístics bàsics
1. Definició d’estadística
En molts manuals sobre estadística hi podem trobar definicions de l’estadística, totes perfectament vàlides i que poden diferir en l’accent que poden posar els autors en un aspecte o un altre de la disciplina. Nosaltres proposem una definició que, sense pretendre que sigui original, creiem que incorpora adequadament tots els trets fonamentals en què tots els autors poden estar d’acord.
Estadística
Conjunt de teories i tècniques que tenen com a objectiu l’organització, presentació, descripció i anàlisi d’un conjunt de dades obtingudes a partir de poblacions o de mostres que representen les poblacions estudiades.
D’aquesta definició podem extreure les característiques principals de l’estadística, en el sentit de considerar que una part del seu contingut es basa en teories desenvolupades en el si de les Matemàtiques, com ara les teories de la probabilitat o de la mesura, però sens dubte l’estadística té una vessant aplicada molt important, que és la que ens proporciona les tècniques adequades per aconseguir diferents objectius. Aquests objectius es poden centrar en dos aspectes diferents:
-
La mera organització d’un conjunt de dades per simplificar-ne l'anàlisi posterior.
-
La presentació de les característiques principals, mitjançant la representació gràfica o la descripció quantitativa d'aquestes característiques.
Finalment, l’estadística també ens proporciona proves que ens permeten analitzar les dades dins un procés metodològic més ampli d’aplicació del mètode científic per tractar d’obtenir informació amb vista a resoldre problemes de tipus teòric o pràctic.
2. Definició de població, mostra i individu
Ja en la definició anterior hem utilitzat una sèrie de termes o conceptes que, tot i que són d'ús quotidià, requereixen una definició més formal que n'acoti el significat.
Aquests conceptes són els següents:
-
Població
-
Mostra
-
Individu (registre)
-
Paràmetre
-
Estadístic
Població
Grup sencer de subjectes dels quals intentem obtenir informació. En un estudi o una anàlisi estadística, la població és el conjunt, habitualment de subjectes, del qual volem generalitzar els resultats obtinguts. En aquest sentit, la delimitació clara de la població de referència o d’interès de l’estudi (població diana) és un element clau a l’hora de definir l’abast de les conclusions.
Mostra
Part de la població que estudiem amb l’objectiu d’obtenir informació.
En els estudis en què apliquem l’estadística habitualment treballem amb mostres de subjectes o casos, ja sigui per descriure determinades variables d’interès dels subjectes o per tractar d’inferir-ne els valors a escala poblacional. En aquest últim cas, la mostra ha de ser representativa de la població. Les tècniques de mostreig intenten aconseguir l’objectiu d’obtenir mostres representatives.
Individu (registre)
Element de la mostra o de la població. Persona, cas o objecte que conté informació que es vol estudiar.
new_pdf_page
Paràmetre
Propietat descriptiva d’una població. És, per tant, un valor numèric que ens resumeix alguna característica d’aquesta població.
Així, la mitjana d’edat dels habitants de Barcelona, si fos la població del nostre estudi, seria un paràmetre. Els paràmetres se simbolitzen mitjançant lletres gregues, i generalment són desconeguts.
Estadístic
Propietat descriptiva d’una mostra. O sigui, un valor numèric que ens informa d’alguna característica d’una mostra.
En el cas anterior dels habitants de Barcelona, si escollíssim una mostra d’aquests habitants i en calculéssim la mitjana d’edat, el valor obtingut seria un estadístic. Els estadístics se simbolitzen mitjançant lletres llatines.
Així, si volem fer un estudi sobre la població de la comarca del Maresme i seleccionem aleatòriament 1.500 habitants, la nostra població de referència són tots els habitants de la comarca del Maresme, mentre que la mostra són els 1.500 habitants seleccionats, i en què cada un és un individu del nostre estudi. Si en aquesta mostra calculéssim la proporció de població estrangera, aquest valor seria un estadístic, i si a partir de les dades oficials de tots els habitants de la comarca poguéssim obtenir la proporció de població estrangera de tota la comarca, aquest valor seria un paràmetre poblacional.
3. Definició de variable i tipus: qualitatives i quantitatives
En estadística, estudiem i analitzem variables com ara el sexe, la nacionalitat o l’edat dels individus en el cas de l’exemple que hem vist en l’apartat anterior. Segons les característiques que a escala estadística tinguin aquestes variables, la seva descripció i anàlisi es podrà dur a terme amb unes tècniques o unes altres. Per tant, en primer lloc, és important definir clarament què entenem per variable i sobretot tenir clars els criteris de classificació per aplicar-hi els procediments d’anàlisi adequats.
Variable
Qualsevol característica, com a propietat dels elements d’una població o mostra, que es pot manifestar en dues o més modalitats (variants). Per exemple, edat, sexe, opinió sobre una qüestió determinada, etc.
A escala estadística podem diferenciar o classificar les variables en dos tipus diferents:
-
Variables qualitatives (o categòriques): són les característiques que només es poden manifestar mitjançant categories considerades qualitats o atributs. Per exemple, sexe, lloc de residència, etc. En aquest tipus de variables, les modalitats són categories.
-
Variables quantitatives: són les característiques que es poden manifestar i mesurar mitjançant un nombre real. Les modalitats corresponen a nombres reals. Dins d’aquestes variables cal diferenciar entre:
-
Variables quantitatives discretes: els valors que poden presentar només són nombres aïllats. Per tant, entre dos valors consecutius no admeten valors intermedis. Per exemple, nombre de fills.
-
Variables quantitatives contínues: poden presentar valors infinits entre dos valors consecutius. Per exemple, edat, alçada, etc. Les variables contínues, per raons de precisió dels instruments de mesura, es poden considerar a la pràctica variables discretes. De totes maneres, per calcular alguns estadístics és convenient, en alguns casos, diferenciar entre el valor aparent i els límits reals d’aquest valor. Així, el valor aparent 50 (per exemple, una edat de 50 anys) és en realitat un interval entre els valors reals 49,5 i 50,5.
-
4. Escales de mesura
Quan assignem valors numèrics a cada una de les modalitats d'una variable estem generant una escala de mesura. Aquest procés s'aplica d'acord amb unes regles establertes, de les quals s'ocupa la teoria de la mesura.
Dit més formalment, una escala de mesura és un procediment mitjançant el qual es relacionen biunívocament un conjunt de modalitats diferents amb un conjunt de nombres diferents, és a dir, a cada modalitat li correspon un únic nombre, i a cada nombre, una única modalitat.
Així, si assignem un 1 a la modalitat “Gens satisfet” com a resposta a la pregunta sobre satisfacció en els serveis d’una biblioteca pública, un 2 a la resposta “Ni molt ni poc satisfet” i un 3 a la resposta “Molt satisfet”, estem generant una escala de mesura per valorar el grau de satisfacció dels usuaris.
En funció de les relacions que podem comprovar empíricament entre els valors numèrics assignats a les modalitats de l'escala, i els tipus de transformacions que podem fer d’aquests valors, podem distingir quatre tipus d’escales de mesura:
-
Nominals
-
Ordinals
-
D’interval
-
De raó
Escala nominal
L’escala nominal és aquella en la qual només es pot comprovar empíricament si les modalitats són iguals o diferents (relació d’igualtat o de desigualtat). Les transformacions possibles poden ser qualssevol, ja que els nombres o valors numèrics assignats a les modalitats són meres etiquetes de les modalitats o categories.
Per exemple, el municipi de residència d’un grup d’usuaris. Així, podem assignar un 1 als usuaris de Barcelona, un 2 als de Badalona, etc., però també podríem assignar l’1 als de Badalona, el 2 als de Barcelona, etc.
Els nombres no tenen propietats matemàtiques, i en aquest sentit no admeten operacions aritmètiques (suma, resta, etc.).
Escala ordinal
En les escales ordinals, a més de poder comprovar si les modalitats són iguals o diferents, podem saber quines són més grans o prèvies a les altres en cas que siguin diferents. Per tant, els nombres assignats a les diferents modalitats admeten les relacions d’igualtat o de desigualtat i d’ordre. Les transformacions possibles són totes les que mantinguin l’ordenació original.
Per exemple, la numeració dels edificis d’un carrer o l’escala de duresa dels materials.
Els nombres només tenen la propietat matemàtica de la seva ordenació, però tampoc no admeten operacions aritmètiques, ja que no hi ha una mateixa quantitat de modalitat entre valors consecutius de l’escala.
Escala d’interval
En les escales d’interval, a més de poder comprovar empíricament la igualtat o desigualtat i l’ordre, també s’estableix una unitat empírica de mesura que ens permet determinar la distància entre dues modalitats qualssevol. El valor nul de l’escala és designat per convenció (arbitrari).
Les transformacions possibles són les lineals que s’expressen segons l'equació:
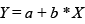
A on X i Y són els diferents valors de les dues escales (la original i la transformada).
Per exemple, l’escala de temperatura, on hi ha una unitat (el grau de temperatura), però el valor 0 es pot situar en diferents punts. Així, en l’escala centígrada o Celsius, el valor de 0 se situa en el punt de congelació de l’aigua, mentre que en l’escala Fahrenheit el 0 se situa en una temperatura més baixa (concretament 31,75 graus centígrads més avall). Pel que fa a les transformacions entre les dues escales de temperatura, si X és el valor en l’escala centígrada i Y el valor corresponent en l’escala Fahrenheit, l’equació lineal que ens permet transformar els graus centígrads en Fahrenheit és la següent: Y = 31,75 + 1,79 X. Els nombres atribuïts a les modalitats mantenen propietats matemàtiques de distància entre valors, d'aquesta manera hi ha la mateixa diferència de temperatura entre 5 i 10 graus centígrads que entre 20 i 25 graus, però no les de raó, perquè les proporcions no es mantenen constants i, per tant, 20 graus no és el doble de temperatura de 10 graus.
Escala de raó
En l’escala de raó, a més de permetre verificar empíricament totes les relacions de les escales anteriors, hi ha un valor nul (no arbitrari) que indica l’absència de la característica que s'ha de mesurar.
Les transformacions possibles són un subconjunt de les lineals on:
![]()
Per exemple, la longitud o el nombre d’usuaris. Així, la longitud la podem mesurar en metres o en peus o en altres unitats, i la transformació d’una en l’altra tan sols requereix conèixer l’equivalent d’una unitat en l’altra. En aquesta última escala de mesura, els nombres atribuïts a les modalitats mantenen totes les propietats matemàtiques, tant de distància entre valors com de proporcions entre ells. D'aquesta manera, hi ha la mateixa distància entre 5 i 10 metres que entre 15 i 20. A més, 20 metres és el doble de distància que 10.
Aquesta tipificació de les escales de mesura es pot relacionar amb la classificació de les variables vista en l’apartat anterior de la manera següent:
-
Les variables qualitatives es poden mesurar en escales nominals (les més habituals) o ordinals.
-
Les variables quantitatives es poden mesurar en escales ordinals, d’interval o de raó (les més habituals).
Unitat 2. Descripció de variables qualitatives
Dades estadístiques
Unitat 2. Descripció de variables qualitatives
1. Introducció
En aquesta unitat presentarem els diferents procediments amb exemples pràctics que permetin un millor seguiment dels continguts treballats.
Per seguir amb més facilitat els diferents apartats que exposarem i que ens serveixin d’activitats no avaluables, recomanem que l’alumne repeteixi amb la matriu de dades del fitxer “dades_alt_penedes.xls”, que forma part del material d’aquest curs, els diferents exemples que es van desenvolupant en aquesta unitat.
Aquests exemples els podreu resoldre amb les opcions i eines estadístiques que ofereix el full de càlcul Excel.
A continuació, us podeu descarregar l’arxiu Excel amb la matriu de dades de l'Alt Penedès que us serviran per fer les activitats pràctiques: Matriu de dades de l’Alt Penedès
A la unitat introductòria d’aquest curs teniu una introducció general a l'ús d’aquest full de càlcul, amb un èmfasi especial a les opcions d'anàlisi estadística.
2. Taules de freqüències
Per organitzar i presentar les dades d’una variable qualitativa, el més habitual és utilitzar una taula de freqüències.
Les taules de freqüències ens proporcionen informació sobre els diferents valors, modalitats o categories de la variable, i el recompte absolut o relatiu del nombre de casos de cada categoria.
2.1. Freqüències absolutes i relatives
Si volem obtenir la taula de freqüències del sexe de la mostra de 1.046 subjectes de la matriu de dades “dades_alt_penedes”, la millor alternativa amb l’Excel és utilitzar l’opció de “Histograma” dins els programes preconfigurats d’anàlisi de dades.
A continuació, farem una activitat pas a pas per posar en pràctica les taules de freqüència.
Aquesta activitat consisteix a seguir unes indicacions pas a pas a fi d'obtenir la taula de freqüències del sexe de la mostra anterior. Per poder-ho fer, us heu de descarregar el següent document.
Un cop hàgiu seguit els passos anteriors i aplicat les modificacions a la matriu, la taula de freqüències definitiva i el gràfic corresponent que obtindreu seran els següents:
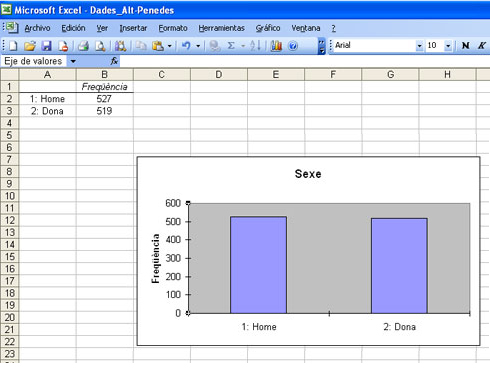
Un cop hem obtingut el resultat, ja podem copiar en qualsevol document tant la taula de freqüències com el diagrama de barres.
Freqüències absolutes
Les freqüències que apareixen en la taula que acabem de crear són les anomenades “freqüències absolutes”, ja que són el recompte del nombre de casos de cada categoria de la variable en la mostra estudiada. Aquestes freqüències se simbolitzen habitualment com “fi”. El sumatori d’aquestes freqüències absolutes ha de donar, si no hi ha cap cas sense valor, el nombre total de subjectes. En aquest exemple, el total seran els 1.046 subjectes de la mostra.
fi = Freqüència absoluta
Recompte del nombre de casos de cada categoria de la variable en la mostra estudiada.
Freqüències relatives
De totes maneres, ens pot ser útil, per raons que exposarem més endavant, obtenir també les anomenades “freqüències relatives”. Les freqüències relatives i els símbols que s'utilitzen habitualment per representar-les són els següents:
Freqüències relatives en proporcions
pi = Freqüència relativa en proporcions
Proporció, o sigui tant per u, del nombre de casos (subjectes) de cada categoria sobre el total de la mostra.
La freqüència relativa en proporcions s’obté dividint la freqüència absoluta de cada categoria pel total de casos o subjectes. El sumatori total d’aquestes freqüències ha de ser igual a 1.
pi = Freqüència relativa en proporcions
![]()
En l'exemple, calcularíem la proporció d’homes de la manera següent:
![]()
Freqüències relatives en percentatges
Pi = Freqüència relativa en percentatges
Percentatge, o sigui tant per cent, del nombre de casos (subjectes) de cada categoria sobre el total de la mostra.
S’obté dividint la freqüència absoluta de cada categoria pel total de casos o subjectes, i multiplicant el resultat per cent. El sumatori total d’aquestes freqüències ha de ser igual a 100.
Pi = Freqüència relativa en percentatges
![]()
En l'exemple, calcularíem el percentatge d’homes de la manera següent:
![]()
La taula de freqüències amb les freqüències absolutes i relatives i els sumatoris de cada una seran els següents:
| Sexe | fi | pi | Pi |
|---|---|---|---|
| 1: Home | 527 | 0,504 | 50,4 |
| 2: Dona | 519 | 0,496 | 49,6 |
| Total | 1046 | 1 | 100 |
Les freqüències relatives seran més útils que les absolutes quan vulguem comparar una mateixa variable obtinguda en mostres de diferents mides. Així, podríem comparar les dades anteriors amb les d’una mostra d’habitants d’alguna altra comarca en què la quantitat fos diferent dels 1.046 de la nostra mostra.
2.2. Freqüències acumulades
Si la variable qualitativa que descrivim està mesurada en una escala ordinal, a més de les freqüències anteriors, absolutes o relatives, també podem obtenir les freqüències acumulades per cada categoria, que ens informaran del nombre de casos o subjectes d’un nivell igual o inferior a una categoria determinada.
Així, en l'exemple podem obtenir les freqüències acumulades per la variable “Edat-2” que hem categoritzat a partir de l’edat dels subjectes. Les instruccions per obtenir la taula de freqüències absolutes amb l’Excel seguiran el mateix format que per conèixer la variable “sexe”, únicament cal tenir en compte que en aquest cas el nombre de categories de la variable és de tres en lloc de les dues de la variable «sexe».
La taula de freqüències d’aquesta variable, amb les absolutes, relatives i acumulades, serà la següent:
| Edat | fi | pi | Pi | fa | pa | Pa |
|---|---|---|---|---|---|---|
| 1: Menors de 16 | 185 | 0,177 | 18 | 185 | 0,177 | 18 |
| 2: Entre 16 i 64 | 702 | 0,671 | 67 | 887 | 0,848 | 85 |
| 3: Majors de 64 | 159 | 0,152 | 15 | 1046 | 1 | 100 |
| Total | 1046 | 1 | 100 |
En aquesta taula de freqüències hem obtingut, a més de les freqüències absolutes i relatives comentades anteriorment, les freqüències acumulades també absolutes o relatives, que són:
fa = Freqüència absoluta acumulada
Recompte del nombre de casos (subjectes) que pertanyen a cada categoria o a categories inferiors.
La freqüència absoluta acumulada s’obté sumant la freqüència absoluta d’una categoria amb les de les categories inferiors. La freqüència absoluta acumulada fins a l'última categoria ha de ser igual al nombre total de casos o subjectes de la mostra.
pa = Freqüència relativa acumulada en proporcions
Proporció, o sigui tant per u, del nombre de casos (subjectes) de cada categoria o de categories inferiors sobre el total de la mostra.
La freqüència relativa acumulada en proporcions s’obté dividint la freqüència acumulada absoluta de cada categoria pel total de casos o subjectes. La freqüència relativa acumulada en proporcions per l'última categoria ha de ser igual a 1.
pa = Freqüència relativa acumulada en proporcions
![]()
En l'exemple, els subjectes entre 16 i 64 anys es calcularien de la manera següent:
![]()
Pa = Freqüència relativa acumulada en percentatges
Percentatge, o sigui tant per cent, del nombre de casos (subjectes) de cada categoria o de categories inferiors sobre el total de la mostra.
La frqüència relativa acumulada en percentatges s’obté dividint la freqüència absoluta acumulada de cada categoria pel total de casos o subjectes, i multiplicant el resultat per cent. La freqüència relativa acumulada en percentatges per l'última categoria ha de ser igual a 100.
Pa = Freqüència relativa acumulada en percentatges
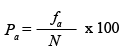
En l'exemple, calcularíem els subjectes entre 16 i 64 anys de la manera següent:
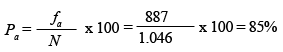
Les freqüències acumulades ens permeten obtenir informació sobre el total o el percentatge de casos, per sobre o per sota d’una determinada categoria.
Així, en l'exemple, podem observar que el 85% dels habitants del Baix Penedès tenen una edat inferior als 65 anys. Com que també es tracta d'una freqüència relativa, ens podria servir per fer una anàlisi comparativa de l’edat dels habitants d’aquesta comarca amb la d’una altra mostra d’habitants d’una comarca diferent, encara que aquesta altra mostra no tingués la mateixa mida que la nostra.
Evidentment, si la variable qualitativa que analitzem no s'hagués mesurat en una escala ordinal, les freqüències acumulades no tindrien cap sentit, ja que l'ordenació de les categories de la variable no seria natural.
3. Representacions gràfiques: diagrama de barres i ciclograma
Les dues representacions gràfiques que s'utilitzen més sovint quan descrivim variables qualitatives són els diagrames de barres i els ciclogrames o diagrames de sectors.
3.1. Diagrama de barres
A partir de la taula que hem elaborat a l'apartat sobre freqüències acumulades, podríem representar el diagrama de barres amb les freqüències acumulades absolutes o relatives d’una variable qualitativa mesurada amb una escala ordinal. Així, per representar el mateix exemple anterior de la variable “Edat-2”, en forma de diagrama de barres amb els percentatges acumulats, ho faríem de la manera següent:
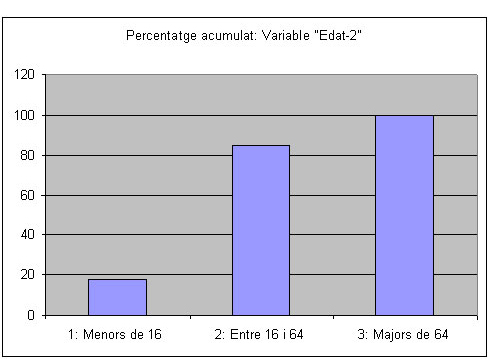
Per dissenyar el diagrama de barres acumulat amb l’Excel podem utilitzar el gràfic de “Columnas”.
En aquesta activitat, us proposem que feu el diagrama anterior seguint un procés pas a pas. Per fer-ho, us heu de descarregar el següent document.
3.2. Ciclograma o diagrama de sectors
L’altra representació gràfica que s'utilitza molt sovint per representar els valors d’una variable qualitativa és el ciclograma o diagrama de sectors.
Els passos que cal seguir per dibuixar un ciclograma són els següents:
-
Dibuixem una circumferència.
-
Dins la circumferència, repartim una porció d’àrea per cada categoria que sigui proporcional a la freqüència absoluta (o relativa) d’aquella categoria.
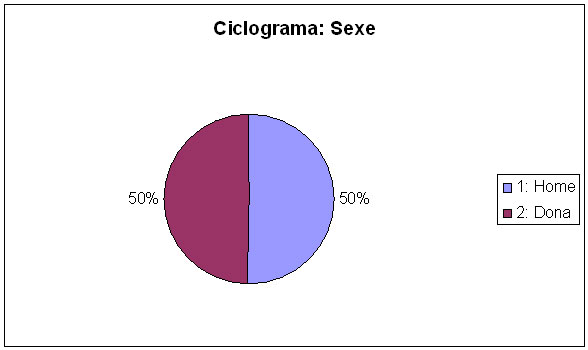
En aquesta activitat, us proposem que feu el ciclograma anterior seguint un procés pas a pas. Per fer-ho, us heu de descarregar el següent document.
Unitat 3. Descripció de variables quantitatives
Dades estadístiques
Unitat 3. Descripció de variables quantitatives
1. Introducció
Ja hem comentat anteriorment que les variables quantitatives permeten un ventall de possibilitats d’anàlisi estadística més ampli que les variables qualitatives, sobretot pel que fa al càlcul de valors representatius que resumeixin característiques concretes de les variables.
Així, en aquesta unitat:
-
Veurem com podem adaptar les taules de freqüències exposades en la unitat anterior en l'apartat de variables quantitatives.
-
Comentarem les representacions gràfiques que s’utilitzen més habitualment per estudiar aquests tipus de variables.
-
Presentarem els diferents indicadors estadístics que ens permeten resumir en un sol valor algunes característiques de les distribucions de variables quantitatives. Les característiques poden ser la centralitat o la tendència central, la variabilitat o la dispersió, l'ordre, la posició o la forma.
Com hem comentat en la unitat anterior, la metodologia de treball per fer un seguiment correcte dels diferents apartats que anirem exposant requereixen que l’alumne faci totes les anàlisis estadístiques, proposades com a exemples, del fitxer “dades_alt_penedes.xls” que formen part del material del curs.
A continuació, us podeu descarregar l’arxiu Excel amb la matriu de dades de l'Alt Penedès que us serviran per fer les activitats pràctiques: Matriu de dades de l’Alt Penedès
2. Taula de freqüències
En la unitat anterior hem definit què entenem per taula de freqüències. Si ho recordem, dèiem:
Les taules de freqüències ens proporcionen informació sobre els diferents valors, modalitats o categories de la variable i el recompte, absolut o relatiu, del nombre de casos de cada categoria.
De totes maneres, si la variable que estem analitzant és quantitativa el nombre de valors que habitualment assumirà en la mostra serà elevat i, per tant, la taula de freqüències amb cada un dels valors com a modalitats de la variable no es podrà fer servir. No obstant això, es pot utilitzar la taula de freqüències per organitzar i presentar les dades d’una variable quantitativa, però en aquest cas agruparem els valors de la variable en intervals o classes.
Per exemple, pensem en l’edat dels habitants de l’Alt Penedès de la mostra que tenim, que va d'1 a 97 anys; és a dir, 97 valors diferents.
Com podríem simplificar la taula de valors de l'exemple anterior perquè sigui manejable?
Podríem agrupar l’edat dels 1.046 habitants de l’Alt Penedès de la mostra en intervals de 15 anys (d'1 a 15 anys, de 16 a 30, de 31 a 45, de 46 a 60, de 61 a 75 i majors de 75). La taula de freqüències resultant serà operativa perquè tindrà sis categories diferents com a intervals d’edat.
Cal tenir present que agrupar els valors d’una variable quantitativa en intervals és un recurs que ens pot ser útil per organitzar, presentar i representar gràficament les dades. Però té un inconvenient: si analitzem posteriorment les dades agrupades, perdrem informació sobre els valors reals de la variable i, segurament, cometrem errors d’agrupació que poden ser més o menys rellevants en funció de l’amplitud dels intervals. Per tant, sempre és millor analitzar posteriorment la variable a partir dels valors originals no agrupats.
Aquesta activitat consisteix a seguir unes indicacions pas a pas a fi d'obtenir la taula de freqüències de l'exemple anterior. Per fer-ho, heu de descarregar el següent document.
Un cop hàgiu seguit els passos anteriors i aplicat les modificacions a la matriu, la taula de freqüències definitiva i la representació gràfica corresponent que obtindreu seran les següents:
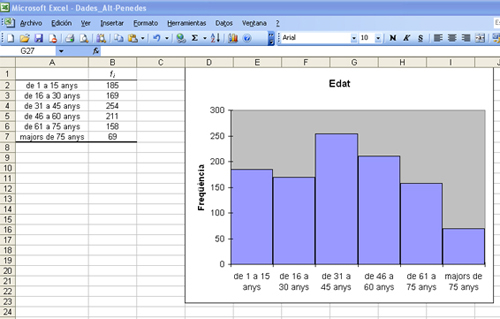
3. Representacions gràfiques: histograma i polígon de freqüències
3.1. Histograma
L'histograma és una representació gràfica que ens informarà, mitjançant una sèrie de columnes, de les freqüències absolutes o relatives de cada un dels intervals o classes de la variable quantitativa agrupada.
L'histograma, molt similar al diagrama de barres de les variables qualitatives, té com a característica diferencial que els rectangles corresponents a cada interval estan units, a diferència del diagrama de barres, en què estan separats.
Això és coherent amb el fet que:
-
Les categories d’una variable qualitativa són valors discrets i separats.
-
Els valors de la variable quantitativa són continus.
A continuació veurem, pas a pas, com podem obtenir l'histograma amb els rectangles adjacents units.
En aquesta activitat us proposem que obtingueu l'histograma de l'exemple amb els rectangles adjacents units. Per fer-ho, heu de descarregar el següent document.
A partir de la taula de freqüències i de l'histograma obtinguts, podem descriure l’edat de la mostra de 1.046 habitants de la comarca de l’Alt Penedès.
Així podem assegurar, per exemple, que el percentatge més gran d’habitants (quasi un 25%) se situa en una franja d’edat d'entre 30 i 45 anys. Que un 18% tenen menys de 16 anys i que un 7% són majors de 75 anys.
D'altra banda, en determinats estudis també ens pot ser útil obtenir la representació gràfica de l'histograma, però a partir dels percentatges acumulats. Seguirem les instruccions que ja hem comentat pel cas d’una variable qualitativa, i n'obtindrem la representació gràfica a través de la pantalla següent:
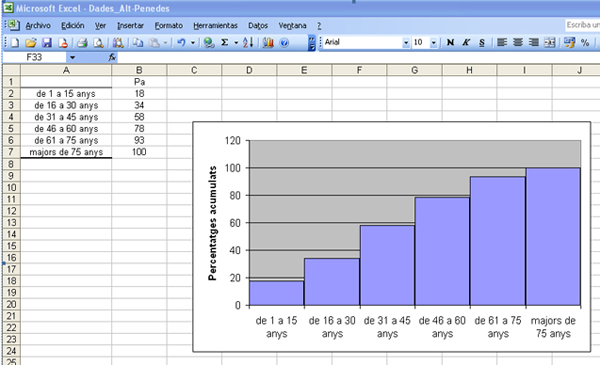
3.2. Polígon de freqüències
El polígon de freqüències és una gràfic derivat de l'histograma. Per obtenir-lo, només cal que unim mitjançant unes línies rectes el punt mitjà de les bases superiors dels rectangles de l'histograma.
En aquesta activitat us proposem que obtingueu el polígon de freqüències de l'exemple. Per fer-ho, heu de descarregar el següent document.
Si observem el gràfic que hem obtingut, podem concloure que el nombre més gran d’habitants tenen una edat compresa entre els 31 i els 45 anys, i el nombre més petit tenen una edat superior a 75 anys.
4. Indicadors estadístics
En una distribució de dades d’una variable quantitativa podem estudiar-hi diferents característiques a partir del càlcul de indicadors de cada una.
Els indicadors o estadístics són valors numèrics que resumeixen el comportament del conjunt de dades de la distribució. Els valors obtinguts per cada un d’aquests indicadors o estadístics ens permetran interpretar alguna d’aquestes característiques i, per tant, ens permetran descriure la variable analitzada.
Les diferents característiques són:
-
La tendència central (centralització)
-
La variabilitat o dispersió
-
L’ordre o la posició
-
La forma
-
La simetria
-
L’apuntament o la curtosi
-
Per obtenir aquests indicadors podem utilitzar les funcions de l’Excel.
En aquesta activitat us proposem que obtingueu els indicadors de l'exemple. Per fer-ho, heu de descarregar el següent document.
De totes maneres, com veurem al final d’aquest apartat, l’Excel també incorpora un programa preconfigurat que ens proporciona un resum dels indicadors.
4.1. Tendència central o centralització: mitjana, mediana i moda
Els indicadors de tendència central ens informen del punt central de la distribució de les dades de la variable estudiada. Són valors numèrics que representen o resumeixen amb una sola dada el centre de la distribució.
Els més utilitzats són:
-
La mitjana aritmètica
-
La mediana
-
La moda
Mitjana aritmètica o mitjana (X)
La mitjana és l'indicador més utilitzat per resumir la tendència central de la distribució d’una variable quantitativa.
La mitjana aritmètica correspon al centre matemàtic dels valors de la distribució.
La mitjana es representa amb el símbol 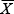 , i es calcula sumant tots els valors de la distribució i dividint el resultat pel nombre de valors o dades.
, i es calcula sumant tots els valors de la distribució i dividint el resultat pel nombre de valors o dades.
La fórmula és:
![]()
Cada Xi representa cada una de les dades de la distribució i «n», el nombre total de dades.
En aquesta activitat obtindrem, pas a pas, la mitjana aritmètica mitjançant l’Excel i utilitzant la funció “PROMEDIO”. Per fer-ho, heu de descarregar el següent document.
Un cop extreta la mitjana, podrem afirmar que el valor obtingut, 40,71 anys, és el més representatiu del conjunt de tots els valors de la variable, i resumeix el punt central de les edats de tots els subjectes de la mostra.
Matemàticament, la mitjana té com a característica més destacable que si sumem totes les diferències entre cada valor de la distribució i la mitjana (el que anomenen puntuacions de desviació), la suma serà igual a zero. Així, si calculéssim la diferència entre cada edat dels 1.046 subjectes de la mostra i la mitjana de 40,71, i suméssim totes les diferències, el resultat seria igual a zero. Lògicament, es produeix aquest resultat perquè la mitjana és el centre matemàtic de la distribució de les dades.
Dit d'una manera més formal, aquesta propietat seria:
![]()
Mediana (Md)
La mediana és el valor de la distribució que, un cop ordenades les dades de menor a major, deixa un 50% de dades per sota i l’altre 50% per sobre.
Dit d’una altra manera, la mediana divideix la distribució de dades en dues meitats:
-
La meitat de valors per sota la mediana.
-
La meitat de valors per sobre.
Per tant, per obtenir la mediana només haurem de buscar, un cop hem ordenat les dades de la variable estudiada, la puntuació que ocupa la posició:
![]()
Així, seguint amb l'exemple, si tenim els 1.046 habitants de la mostra d’habitants de l’Alt Penedès i volem obtenir la seva mediana d’edat, buscarem la puntuació que ocupa la posició: ![]()
![]()
O sigui, el punt mitjà entre les puntuacions que ocupen, un cop ordenades les dades de menys edat a més, les posicions 523 i 524.
En aquesta activitat obtindrem, pas a pas, la mediana mitjançant l’Excel i utilitzant la funció “MEDIANA”. Per fer-ho, heu de descarregar el següent document.
Un cop hem obtingut la mediana, podrem interpretar el valor en el sentit que, en la mostra d’habitants de l’Alt Penedès, la meitat tenen menys de 40 anys i l’altra meitat, més de 40.
La mediana té una característica que no té la mitjana aritmètica, i que en alguns casos la pot fer més representativa o útil que la mateixa mitjana. Aquesta característica és l'anomenada robustesa.
La robustesa fa referència al fet que la mediana no es veu afectada per possibles valors extrems o atípics de la distribució de dades.
Així, tant si l’edat de l’habitant de més edat de la mostra fos de 97 anys, com és el cas, com si fos de 120, la mediana continuaria sent 40, ja que aquest valor extrem (120) no repercuteix sobre el valor de la mediana.
La mitjana es veuria afectada per aquest valor extrem de 120, encara que en l'exemple, com que la mostra és d'una mida considerable, un sol valor atípic o extrem tampoc no repercutiria de manera rellevant sobre la mitjana.
De totes maneres, cal tenir en compte aquesta característica de la mediana a l’hora de decidir quin pot ser l'indicador de tendència central més representatiu d’una distribució de dades:
-
Si la distribució presenta valors extrems o atípics (el que anomenem distribució asimètrica), la mediana pot ser més representativa de la tendència central de les dades que la mitjana aritmètica.
-
Si, com és el cas de l'exemple, la mediana i la mitjana tenen valors molt propers (40 i 40, 71), podem interpretar-ho com que la distribució de dades de la variable és força simètrica i, per tant, no hi ha valors atípics o extrems (valors molt allunyats de la resta de valors de la variable), i en aquest cas la mitjana aritmètica serà l'indicador de tendència central més representatiu.
Tornarem a tractar el tema de la simetria en l’apartat dels indicadors de forma.
Moda (Mo):
La moda és el valor més freqüent d’una distribució de dades.
Podem identificar diferents tipus de distribucions en funció de la moda:
-
Amodal: si no hi ha cap valor que es repeteixi més que els altres.
-
Multimodals (bimodals, trimodals, etc.): distribucions que tinguin més de una moda.
Per obtenir la moda amb l’Excel, utilitzem la funció “MODA”, seguim les indicacions ja exposades per els indicadors anteriors.
Així, en el cas del nostre exemple, la moda de la mostra d’habitants de l’Alt Penedès és de 40 anys. Si agrupéssim els subjectes per edats, podríem comprovar que els subjectes de 40 anys son el més nombrosos (21 subjectes).
La moda no és un indicador molt utilitzat per caracteritzar la tendència central de una distribució, però pot ser útil per obtenir un perfil característic d’una mostra de dades. Així, si tractéssim d’obtenir el perfil o prototip d’edat dels habitants de l’Alt Penedès, podríem dir que és una persona de 40 anys.
Criteris per triar l'indicador de tendència central més adequat
-
L'indicador de tendència central més utilitzat i més representatiu per a variables quantitatives és la mitjana.
-
De totes maneres, com hem comentat anteriorment, si la distribució de la variable estudiada és força asimètrica (o sigui, que tingui valors extrems o atípics), la mediana pot ser més representativa que la mitjana, ja que no es veu afectada pels valors extrems. En aquests casos, és aconsellable indicar els dos valors (mitjana i mediana) per interpretar de manera més adequada la centralitat de la distribució de dades.
-
També cal tenir en compte que si la variable és qualitativa mesurada amb una escala ordinal, no podem calcular la mitjana aritmètica i, per tant, l'indicador de tendència central més adequat serà la mediana.
-
Finalment, la moda només té sentit en la descripció de variables qualitatives mesurades amb escales nominals (ja que és l’únic indicador calculable), i en determinats casos en què l’objectiu és obtenir un perfil característic o prototípic d’una determinada variable.
4.2. Variabilitat o dispersió: variància, desviació típica i coeficient de variació
Sovint, per descriure una distribució de dades d’una variable quantitativa, no n'hi ha prou de calcular i interpretar algun indicador de tendència central, ja que aquest identifica el valor central més representatiu però no ens aporta informació respecte als altres valors de la variable.
Per exemple, podem tenir dues mostres d’habitants de dues ciutats diferents amb una mateixa mitjana d’edat (suposem, de 40 anys), però en què la resta de valors de les edats dels habitants són molt semblants entre ells en una ciutat o molt dispersos en l’altra. La característica de la variabilitat o dispersió de les dades ens permet interpretar si la mostra és molt homogènia respecte a la variable que estudiem (molts habitants amb edats similars), o molt heterogènia (habitants amb moltes diferències d’edat).
Els indicadors de variabilitat o dispersió més utilitzats són:
-
La variància
-
La desviació típica
-
El coeficient de variació
Els indicadors de dispersió s'obtenen del càlcul de les anomenades puntuacions diferencials.
Una puntuació diferencial és la diferència entre un dels valors de la variable i la mitjana de tots els valors.
Formalment:
![]()
On identifiquem amb x minúscula la puntuació diferencial i X majúscula la puntuació directa.
Així, aplicant-ho a l'exemple, per al primer subjecte de la matriu de dades dels 1.046 habitants de la comarca de l’Alt Penedès la puntuació diferencial (o de diferència) de l’edat és de -22,71 anys.
Per al primer subjecte de la matriu de dades:
![]() Això vol dir que el primer subjecte s’allunya 22,71 anys de la mitjana d’edat de tots els subjectes de la mostra.
Això vol dir que el primer subjecte s’allunya 22,71 anys de la mitjana d’edat de tots els subjectes de la mostra.
Sembla evident que com més elevades són les puntuacions diferencials, més dispersa és la característica que estem estudiant (més diferències hi ha entre cada puntuació i la mitjana de totes); i com més baixes són les puntuacions de diferència, menys dispersa és la mostra respecte a aquesta característica (en l’exemple: l’edat). Per tant, a partir de les puntuacions diferencials podrem obtenir indicadors que ens permetin interpretar si la distribució de valors de la variable és més o menys dispersa.
De totes maneres, a l’hora de sumar totes les puntuacions de diferència d’una variable ens trobem que, com a conseqüència de la característica esmentada de la mitjana, el sumatori és igual a zero.
El recurs per obtenir un indicador de variabilitat a partir de les puntuacions diferencials és elevar al quadrat les puntuacions de diferència, amb la qual cosa se soluciona el problema del valor nul del sumatori.
Variància (S²)
La variància és la mitjana de la puntuacions diferencials elevades al quadrat. O sigui, que s’obté sumant els quadrats de les puntuacions diferencials i dividint el resultat pel nombre de puntuacions.
En aquest punt, cal tenir en compte que podem diferenciar entre dues fórmules, lleugerament diferents, de calcular la variància. El perquè d’aquestes dues formes de càlcul queda fora de l’abast del curs, ja que és una qüestió d’estadística inferencial.
Les dues fórmules de càlcul permeten diferenciar entre el que habitualment es considera:
-
Variància mostral
-
Variància poblacional
La més utilitzada és la variància mostral, i la fórmula per calcular-la és la següent:
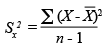
La variància poblacional només es diferencia pel fet que en lloc de dividir-se per «n-1», es divideix per «n». Si la mida de la mostra és elevada, la diferència entre els valors de les dues variàncies serà mínima.
Per obtenir la variància mitjançant l’Excel utilitzem la funció VAR. Seguint la seqüència d’instruccions descrita pels indicadors de tendència central, si calculem la variància de l’edat de la mostra de 1.046 habitants de l’Alt Penedès obtindrem un valor de 506,80. Aquest valor correspondria a la fórmula següent:
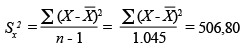
Si volguéssim obtenir la variància poblacional, utilitzaríem la funció VARP, que en l'exemple ens donaria un valor de 506,32 que, com podem comprovar, és gairebé igual que l'obtingut anteriorment.
A l’hora d'interpretar el valor de la variància, ens trobem amb la dificultat que s'ha calculat elevant al quadrat les puntuacions de diferència, i, per tant, les unitats són les pròpies de la variable estudiada però elevades al quadrat.
Així, en l'exemple, no podem concloure que la variabilitat o la dispersió de l’edat dels habitants de l’Alt Penedès sigui de 506 anys, ja que la xifra és clarament exagerada perquè no són 506 anys, sinó 506 anys al quadrat.
Per aquest motiu, l'indicador de variabilitat o dispersió més utilitzat no és la variància, sinó la desviació típica, que no és altra cosa que l’arrel quadrada de la variància.
Desviació típica o desviació estàndard (S)
La desviació típica o desviació estàndard és l’arrel quadrada de la variància.
D’aquesta manera, tenim un indicador de variabilitat o dispersió que podem interpretar amb les unitats pròpies de la variable estudiada. També, com en el cas de la variància, podem distingir entre la desviació típica mostral (la més habitual) i la poblacional. Tant l'una com l’altra es calculen obtenint l’arrel quadrada de la variància corresponent (ja sigui la mostral o la poblacional).
En el cas de la mostral, la fórmula per calcular-la serà:
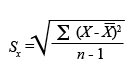
Podem obtenir la desviació típica mitjançant l’Excel utilitzant la funció DESVEST.
Continuem amb l'exemple. Si calculem la desviació típica de l’edat dels 1.046 habitants de l’Alt Penedès, obtindrem un valor de 22,51. El valor correspondria a la fórmula següent:
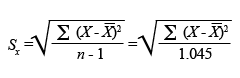 Per obtenir la desviació estàndard poblacional, utilitzarem la funció DESVESTP, que en l'exemple ens dóna un valor de 22,50.
Per obtenir la desviació estàndard poblacional, utilitzarem la funció DESVESTP, que en l'exemple ens dóna un valor de 22,50.
Com en el cas de la variància, els valors mostral i poblacional són pràcticament iguals, ja que el nombre de subjectes de la mostra (n) és elevat.
El valor de l'indicador de variabilitat ja es pot interpretar en les unitats pròpies de la variable estudiada.
D'aquesta manera, podem concloure que en l'exemple la dispersió o variabilitat de les edats de la mostra d’habitants de l’Alt Penedès correspon a una desviació típica de 22 anys i mig. El resultat ja és molt més representatiu de la dispersió de les dades de les edats de la mostra, a diferència dels 506 anys de la variància.
Coeficient de variació (CV)
Si la desviació típica és un indicador de variabilitat absolut, ja que s'expressa en funció de les unitats de la variable estudiada, el coeficient de variació és un indicador de variabilitat relatiu ja que representa el percentatge de variació respecte a la mitjana de la distribució. Així, el coeficient de variació ens serà útil quan vulguem comparar la variabilitat de dues variables diferents o de la mateixa variable en dues mostres amb mitjanes diferents.
La fórmula per calcular el coeficient de variació és la següent:

El coeficient de variació s’interpreta com un percentatge de variabilitat respecte a la mitjana de la distribució, i com més dispersió presenti la variable estudiada més elevat serà.
L’Excel no té cap funció per calcular directament el coeficient de variació, però el podrem obtenir fàcilment a partir de la seva fórmula.
Així, en l’exemple de l’edat dels habitants de l’Alt Penedès, el coeficient de variació serà:

Per tant, podem concloure que la dispersió de l’edat de la mostra de subjectes és d’un 55% respecte a la mitjana, que podem interpretar com una dispersió o variabilitat mitjana.
4.3. Ordre o posició
Els indicadors d’ordre o posició ens seran útils quan vulguem determinar quin percentatge de subjectes estan per sota o per sobre d’un determinat valor de la variable, o per conèixer el valor que deixa per sota un determinat percentatge de casos o subjectes.
Així, en l'exemple dels habitants de l’Alt Penedès, ens podria interessar determinar quin percentatge d’habitants tenen menys de 25 anys, o quina edat ens deixa un 20% d’habitants per sobre d'aquesta edat. Dit d’una altra manera, si volem triar el 20% d’habitants amb més edat, a partir de quina edat els hauríem de seleccionar.
L'indicador d’ordre o posició més habitual és el percentil, encara que també s’utilitza un indicador derivat d'aquest mateix indicador, el quartil.
Percentil (Pc)
Els percentils són els valors de la distribució de dades que, un cop ordenades de menor a major, deixen un percentatge determinat de casos o subjectes per sota.
Els percentils tenen un rang de valors d'1 a 100. Així, el percentil 30 és el valor de la distribució que deixa un 30% de les dades per sota i, evidentment, un 70% per sobre.
Per tant, en els exemples que exposàvem anteriorment, per determinar quin percentatge d’habitants de l’Alt Penedès tenen menys de 25 anys, hauríem de calcular quin percentil correspon a una edat de 25 anys; i si volem triar el 20% d’habitants amb més edat, haurem de buscar quina edat correspon al percentil 80, que és el que deixa per sobre un 20% de casos amb valors més elevats.
Per obtenir un percentil amb l’Excel, utilitzarem la funció PERCENTIL.
Si, com en l'exemple, volem obtenir el percentil 80 de la mostra d’habitants de l’Alt Penedès, seguirem la seqüència d’instruccions coneguda per activar una funció: “Insertar”, “Función”, “PERCENTIL”, i en el quadre de diàleg que apareixerà hi inclourem:
-
A “Matriz”, les caselles de valors de la variable estudiada.
-
A “k”, el valor del percentil dividit per 100 (en l'exemple, 0,8).
I quedarà de la manera següent:
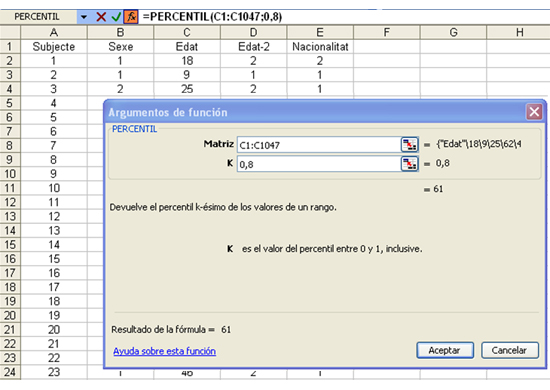
Com podem observar, el percentil 80 de l’edat de la mostra d’habitants de l’Alt Penedès és 61, resultat que ens confirma que el 20% d’habitants de més edat es troben per sobre de 61 anys. O dit d’una altra manera, que el 80% d’habitants tenen 61 anys o menys.
D'altra banda, per determinar quin percentil correspon a un valor determinat de la variable, utilitzarem la funció RANGO.PERCENTIL.
Així, per determinar quin percentatge d’habitants de l’Alt Penedès tenen menys de 25 anys activarem la funció anterior, i escriurem el següent en el quadre de diàleg:
-
A “Matriz”, les caselles de les dades de la variable.
-
A “X”, el percentil que busquem.
-
A “Cifra-significativa” no cal incloure-hi cap valor, ja que l’Excel ens proporcionarà per defecte 3 decimals.
La pantalla corresponent serà:
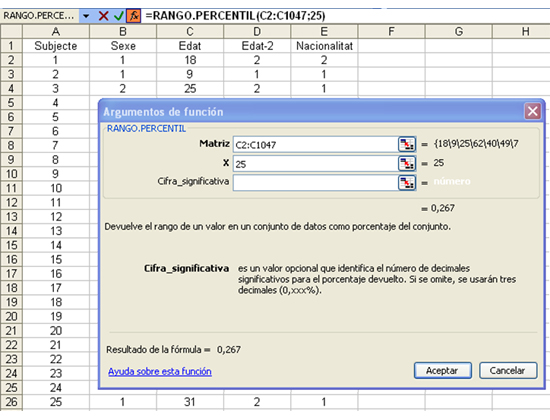
El resultat que ens dóna l’Excel és de 0,267. Per obtenir el percentil, multiplicarem el valor per cent i l’arrodonirem a l’enter més pròxim.
Així, en l'exemple, el percentil que correspon a una edat de 25 anys és el 27. Per tant, podem concloure que el 27% d’habitants de l’Alt Penedès tenen 25 anys o menys, i el 73% restant, més de 25.
Els quartils (Q)
Si els percentils divideixen la distribució en 100 parts iguals, el quartils ho fan en 4 parts iguals.
Així, tindrem quatre tipus de quartils:
-
El quartil 1 (Q1) és el valor de la distribució que deixa per sota, un cop ordenades les dades de menor a major, el 25% de casos o subjectes.
-
El quartil 2 (Q2) deixa per sota un 50% de casos.
-
El quartil 3 (Q3) que deixa un 75% de casos per sota.
-
El quartil 4 és el valor màxim de la distribució.
Com podem observar, de fet, els quartils són uns percentils determinats. El quartil 1 és el percentil 25, el quartil 2, el percentil 50, i el quartil 3, el percentil 75.
La mediana, a més de ser un indicador de tendència central, també és un indicador de posició ja que es correspon amb el percentil 50 i amb el quartil 2.
Per obtenir els diferents quartils amb l’Excel utilitzarem la funció “CUARTIL”. En el quadre de diàleg d’aquesta funció, hem d'introduir-hi les caselles de la variable que volem estudiar a “Matriz” i el quartil que volem obtenir a “Cuartil”.
Per obtenir el tercer quatil de l'exemple de la mostra d’habitants de l’Alt Penedès, hem de seguir els passos següents. Omplirem el quadre tal com mostra la captura de pantalla següent:
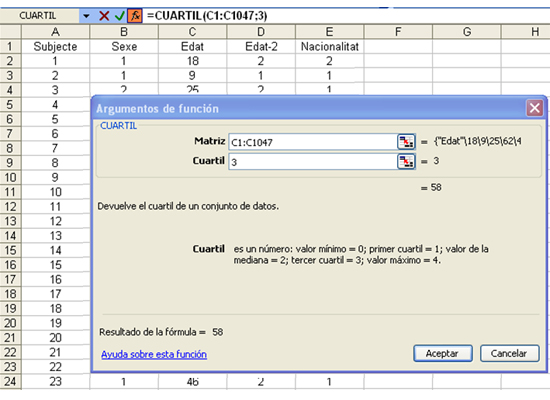
Com podem comprovar, el tercer quartil correspon a una edat de 58 anys. Podem concloure que el 75% d’habitants de la comarca tenen una edat igual o inferior als 58 anys, i un 25%, una edat superior al 58.
4.4. Forma: simetria i curtosi
Els indicadors de forma no són tan utilitzats per descriure una variable quantitativa però ens poden ser útils, en alguns casos, per determinar l'adequació d'un indicador o un altre.
En els indicadors de forma, podem distingir entre:
-
Els de simetria
-
Els de curtosi o apuntament
new_pdf_page
Coeficient d'asimetria (As)
La simetria de les dades d’una variable té a veure amb la distribució dels valors a una banda i a l'altra de la tendència central.
-
La distribució serà simètrica quan els valors per sota i per sobre de la mitjana segueixin un comportament similar (gràficament, tenen una forma similar).
-
La distribució serà asimètrica quan els valors per sobre o per sota del punt mitjà tinguin un comportament diferent (gràficament, tenen una configuració diferent).
Un gràfic com l'histograma pot ser força informatiu sobre la possible simetria o asimetria de la distribució. L'asimetria pot ser:
-
Positiva: si hi ha més casos en el rang de valors inferiors.
-
Negativa: si hi ha més casos en el rang de valors superiors.
Així, els tres histogrames següents corresponents a dues distribucions asimètriques (positiva o negativa) i una de simètrica:
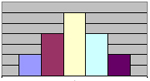 Simetria
Simetria
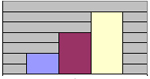 Asimetria negativa
Asimetria negativa
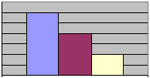 Asimetria positiva
Asimetria positiva
Hi ha diferents indicadors de simetria, però aquí només exposarem el que podem obtenir mitjançant l’Excel.
Correspon a la fórmula següent:
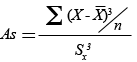
La funció de l’Excel que ens permet obtenir aquest indicador de simetria és: COEFICIENTE.ASIMETRIA.
Com més proper a zero sigui el valor del coeficient d'asimetria, més simètrica serà la distribució, i com més s’allunyi de zero més asimètrica serà, ja sigui en sentit positiu com correspon a una asimetria positiva, o sigui en sentit negatiu com correspon a una asimetria negativa.
En l'exemple, el coeficient d’asimetria obtingut amb l’Excel ens dóna un valor de 0,12.
Un coeficient d’asimetria de 0,12 el podem interpretar com una distribució força simètrica.
Curtosi o apuntament (Cr)
Si la distribució és simètrica també es pot obtenir una nova característica de la forma de la distribució, l'anomenada curtosi.
La curtosi o apuntament reflecteix la concentració de valors pròxims a la tendència central.
Així, si hi ha molts valors concentrats a prop de la mitjana de la distribució, la forma de l'histograma serà apuntada, mentre que si el valors no es concentren al voltant de la mitjana, la forma de l'histograma serà aplanada.
Un indicador de curtosi és l’índex d’apuntament, que té la fórmula següent:
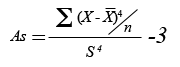
Per obtenir aquest indicador amb l’Excel utilitzarem la funció «CURTOSIS».
Si el valor de l'indicador és pròxim a zero, la distribució serà normal; si és positiu, serà una distribució apuntada, mentre que si és negatiu, serà aplanada.
Si identifiquem aquest indicador en l'exemple, ens dóna un valor de -0,79, xifra que podem interpretar com una distribució de l’edat dels habitants de l’Alt Penedès més aviat aplanada.
5. Resum d’indicadors descriptius d’una variable quantitativa amb l’Excel
L’Excel ens ofereix, dins dels programes preconfigurats, una opció que ens calcula de manera conjunta la major part d’indicadors descriptius comentats en els apartats anteriors. Aquesta opció és molt interessant, ja que ens estalvia la feina d'anar-los obtenint, funció rere funció, un per un.
Per activar aquest opció, hem de seguir la seqüència habitual per a aquests programes preconfigurats: “Herramientas”, “Análisis de datos”, i “Estadística descriptiva” dins les diferents funcions.
Per obtenir el resum d’indicadors descriptius per a la variable “Edat” de l'exemple, omplirem el quadre de diàleg del programa preconfigurat tal com es mostra en la captura de pantalla següent:
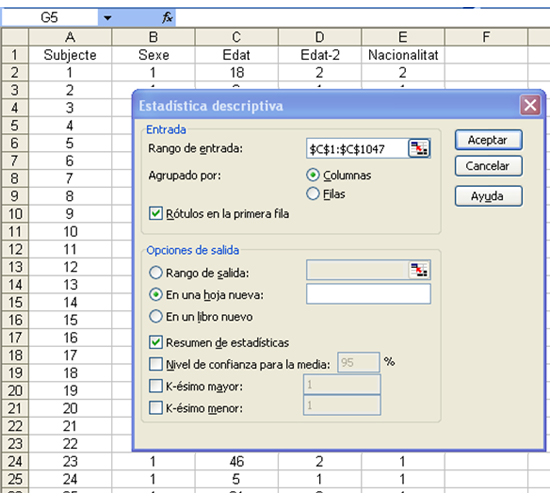
Com podem observar, hem introduït les caselles de la variable al “Rango de entrada”, hem activat l'opció “Rótulos en la primera fila” i també l'opció “Resumen de estadísticas”. Si premem “Aceptar”, l’Excel ens proporcionarà el resum d’indicadors estadístics següent:
| Edat | |
|---|---|
| Media | 40,71 |
| Error típico | 0,70 |
| Mediana | 40 |
| Moda | 40 |
| Desviación estándar | 22,51 |
| Varianza de la muestra | 506,80 |
| Curtosis | -0,79 |
| Coeficiente de asimetría | 0,12 |
| Rango | 96 |
| Mínimo | 1 |
| Máximo | 97 |
| Suma | 42.583 |
| Cuenta | 1.046 |
El resum d’indicadors descriptius que ens ha calculat és el següent:
| Media | Mitjana |
|---|---|
| Error típico | Error típic (utilitzat en estadística inferencial) |
| Mediana | Mediana |
| Moda | Moda |
| Desviación estándar | Desviació típica |
| Varianza de la muestra | Variància |
| Curtosis | Curtosi |
| Coeficiente de asimetría | Asimetria |
| Rango | Rang o amplitud (diferencia entre el valor màxim i el mínim) |
| Mínimo | Valor mínim |
| Máximo | Valor màxim |
| Suma | Suma de tots els valors |
| Cuenta | Nombre de casos o subjectes |
Ja hem comentat la interpretació de cada un dels indicadors quan ens hi hem referit en els apartats anteriors.
Per tant, amb aquesta opció disposem d'un bon resum dels diferents indicadors tant de tendència central, de variabilitat o dispersió, com de forma de la distribució de la variable estudiada, amb l’avantatge que els podem calcular tots conjuntament amb una sola opció. També ofereix l’avantatge que, si haguéssim de descriure diferents variables quantitatives, les podríem incloure totes en el rang d’entrada i el programa ens calcularia el resum d’indicadors descriptius per a cada una.
Fitxes resum
Dades estadístiques
Fitxes resum
Conceptes bàsics
| Estadística | Conjunt de teories i tècniques que tenen com a objectiu l’organització, la presentació, la descripció i l'anàlisi d’un conjunt de dades obtingudes a partir de poblacions o de mostres que representen les poblacions estudiades. |
|---|---|
| Població | Grup sencer de subjectes dels quals intentem obtenir informació. |
| Mostra | Part de la població que estudiem amb l’objectiu d’obtenir-ne informació. |
| Individu (registre) | Element de la mostra o de la població. Persona, cas o objecte que conté informació que es vol estudiar. |
| Paràmetre | Propietat descriptiva d’una població. És, per tant, un valor numèric que resumeix alguna característica de la mateixa població. |
| Estadístic | Propietat descriptiva d’una mostra. O sigui, un valor numèric que ens informa d’alguna característica d’una mostra. |
| Variable | Qualsevol característica, com a propietat dels elements d’una població o mostra, que es pot manifestar en dues o més modalitats (variants). Per exemple: edat, sexe, opinió sobre una qüestió determinada, etc. |
| Variables qualitatives | Són les característiques que només es poden manifestar mitjançant categories considerades qualitats o atributs. Per exemple: sexe, lloc de residència, etc. Les modalitats són categories. |
| Variables quantitatives | Són les característiques que es poden manifestar i mesurar mitjançant un nombre real. Les modalitats corresponen a nombres reals. |
| Variables quantitatives discretes | Els valors que poden presentar només són nombres aïllats. Per tant, entre dos valors consecutius no admeten valors intermedis. Per exemple: nombre de fills. |
| Variables quantitatives contínues | Poden presentar valors infinits entre dos valors consecutius. Per exemple: edat, alçada. |
Descripció d’una variable qualitativa
Taula de freqüències
Les taules de freqüències ens proporcionen informació sobre els diferents valors, modalitats o categories de la variable i el recompte absolut o relatiu del nombre de casos de cada categoria.
Exemple 1:
| Sexe | fi | pi | Pi |
|---|---|---|---|
| 1: Home | 527 | 0,504 | 50,4 |
| 2: Dona | 519 | 0,496 | 49,6 |
| Total | 1046 | 1 | 100 |
-
fi = Freqüència absoluta: recompte del nombre de casos de cada categoria de la variable en la mostra estudiada.
-
Obtenció amb l’Excel: programa preconfigurat de “Análisis de datos”: “Histograma”.
-
Freqüència relativa en proporcions (pi): Proporció, o sigui tant per u, del nombre de casos (subjectes) de cada categoria sobre el total de la mostra. S’obté dividint la freqüència absoluta de cada categoria pel total de casos o subjectes:
| Fórmula | |
|---|---|
| Per als homes de l'exemple | |
-
Freqüència relativa en percentatges (Pi): percentatge, o sigui tant per cent, del nombre de casos (subjectes) de cada categoria sobre el total de la mostra. S’obté dividint la freqüència absoluta de cada categoria pel total de casos o subjectes, i multiplicant el resultat per cent:
| Fórmula | |
|---|---|
| Per als homes de l'exemple | |
Exemple 2:
| Edat | fi | pi | Pi | fa | pa | Pa |
|---|---|---|---|---|---|---|
| 1: Menors de 16 | 185 | 0,177 | 18 | 185 | 0,177 | 18 |
| 2: Entre 16 i 64 | 702 | 0,671 | 67 | 887 | 0,848 | 85 |
| 3: Majors de 64 | 159 | 0,152 | 15 | 1046 | 1 | 100 |
| Total | 1046 | 1 | 100 |
-
Freqüència absoluta acumulada (fa): recompte del nombre de casos (subjectes) que pertanyen a cada categoria o a categories inferiors. S’obté sumant la freqüència absoluta d’una categoria amb les de les categories que són inferiors a aquesta mateixa categoria.
-
Freqüència relativa acumulada en proporcions (pa): proporció, o sigui tant per u, del nombre de casos (subjectes) de cada categoria o de categories inferiors sobre el total de la mostra. S’obté dividint la freqüència acumulada absoluta de cada categoria pel total de casos o subjectes:
| Fórmula | |
|---|---|
| Per als subjectes d'entre 16 i 64 anys de l'exemple 2 | |
-
Freqüència relativa acumulada en percentatges (Pa): percentatge, o sigui tant per cent, del nombre de casos (subjectes) de cada categoria o de categories inferiors sobre el total de la mostra. S’obté dividint la freqüència absoluta acumulada de cada categoria pel total de casos o subjectes, i multiplicant el resultat per cent:
| Fórmula | 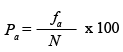
|
|---|---|
| Per als subjectes d'entre 16 i 64 anys de l'exemple 2 | 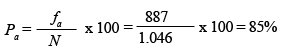
|
Representacions gràfiques
Diagrama de barres
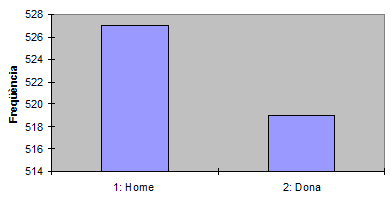
-
Obtenció amb l’Excel: programa preconfigurat de “Análisis de datos”, “Histograma”.
Ciclograma
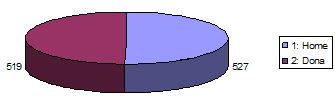
-
Obtenció amb l’Excel: “Insertar”, “Gráfico” i “Circular”.
Descripció d’una variable quantitativa
Taula de freqüències agrupades per intervals o classes
Exemple:
| Edat | fi | pi | Pi | fa | pa | Pa |
|---|---|---|---|---|---|---|
| de 1 a 15 anys | 185 | 0,177 | 18 | 185 | 0,18 | 18 |
| de 16 a 30 anys | 169 | 0,162 | 16 | 354 | 0,34 | 34 |
| de 31 a 45 anys | 254 | 0,243 | 24 | 608 | 0,58 | 58 |
| de 46 a 60 anys | 211 | 0,202 | 20 | 819 | 0,78 | 78 |
| de 61 a 75 anys | 158 | 0,151 | 15 | 977 | 0,93 | 93 |
| majors de 75 anys | 69 | 0,066 | 7 | 1046 | 1 | 100 |
| Total | 1046 | 1 | 100 |
-
Obtenció amb l’Excel: programa preconfigurat de “Análisis de datos”, “Histograma”.
Representacions gràfiques
Histograma
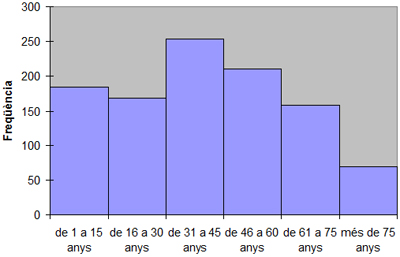
-
Obtenció amb l’Excel: programa preconfigurat de “Análisis de datos”, “Histograma”.
Polígon de freqüències
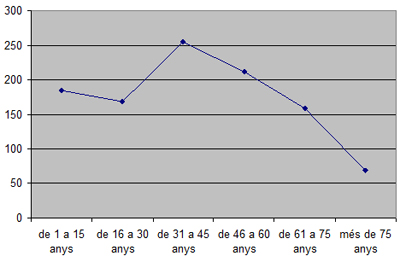
-
Obtenció amb l’Excel: “Insertar”, “Gráfico” i “Líneas”.
Indicadors descriptius
Tendència central (Centralitat)
Mitjana aritmètica o mitjana
(![]() )
)
| Definició | Sumatori de totes les dades de la distribució dividit pel nombre de dades. |
|---|---|
| Ús i interpretació | Indicador més àmpliament utilitzat. Menys representatiu en cas que la distribució sigui força asimètrica. |
| Fórmula | |
| Obtenció amb l’Excel | “Insertar”, “Función” i “PROMEDIO”. |
Mediana (Md)
| Definició | Valor de la distribució que, un cop ordenades les dades de menor a major, deixa un 50% de dades per sota i l’altre 50% per sobre. |
|---|---|
| Ús i interpretació | Indicat si la variable s'ha mesurat amb escala ordinal. Més representatiu que la mitjana si la distribució és força asimètrica. |
| Fórmula | Buscar el valor de la distribució que ocupa la posició |
| Obtenció amb l’Excel | “Insertar”, “Función” i “MEDIANA”. |
Moda (Mo)
| Definició | Valor més freqüent d’una distribució de dades. |
|---|---|
| Ús i interpretació | Útil per a variables qualitatives i en cas que busquem perfils prototípics. |
| Obtenció amb l’Excel | “Insertar”, “Función” i “MODA”. |
new_pdf_page
Variabilitat o dispersió
Variància
(S2)
| Definició | Sumatori de les puntuacions de desviació |
|---|---|
| Ús i interpretació | Menys utilitzat que la desviació típica, ja que les unitats que la componen són les pròpies de la variable al quadrat |
| Fórmula | 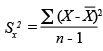 |
| Obtenció amb l’Excel | “Insertar”, “Función” i “VAR”. |
Desviació típica o desviació estàndard (S)
| Definició | Arrel quadrada de la variància. |
|---|---|
| Ús i interpretació | Indicador de dispersió més utilitzat, ja que les unitats que la componen són les pròpies de la variable. |
| Fórmula | 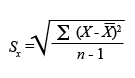 |
| Obtenció amb l’Excel | “Insertar”, “Función” i “DESVEST”. |
Coeficient de variació (CV)
| Definició | Percentatge de variació respecte a la mitjana de la distribució. |
|---|---|
| Ús i interpretació | Indicador de dispersió utilitzat per comparar variabilitats de diferents variables, o de la mateixa variable en mostres amb mitjana diferent. |
| Fórmula |  |
new_pdf_page
Ordre o posició
Percentil
(Pk)
| Definició | Valor de la distribució de dades que, un cop ordenades de menor a major, deixen un percentatge (k) determinat de casos o subjectes per sota. |
|---|---|
| Ús i interpretació | Útil a l'hora de buscar el valor de la distribució que deixa un percentatge determinat de casos per sota o per sobre. |
| Fórmula | Pk: buscar el valor de la distribució que ocupa la posició |
| Obtenció amb l’Excel | “Insertar”, “Función” i “PERCENTIL”. |
Quartils (Q)
| Definició | Si els percentils divideixen la distribució en cent parts iguals, el quartils ho fan en quatre. |
|---|---|
| Ús i interpretació | Igual que els percentils, però deixant un 25, 50 o 75% de casos per sota. |
| Fórmula | Qk: buscar el valor de la distribució que ocupa la posició |
| Obtenció amb l’Excel | “Insertar”, “Función” i “CUARTIL”. |
new_pdf_page
Forma
Coeficient d'asimetria (As)
| Definició | Distribució dels valors a una banda i a l'altra de la mitjana. |
|---|---|
| Ús i interpretació | Útil per estudiar la simetria o asimetria (positiva o negativa) de la distribució i per decidir, en alguns casos, quin serà l'indicador de tendència central més representatiu. |
| Fórmula | 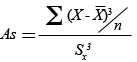 |
| Obtenció amb l’Excel | “Insertar”, “Función” i “COEFICIENTE.ASIMETRIA”. |
Curtosi o apuntament (Cr)
| Definició | Concentració de valors propers a la mitjana. |
|---|---|
| Ús i interpretació | Només és interpretable si la distribució és simètrica i ens permet determinar si és aplanada, normal o apuntada. |
| Fórmula | 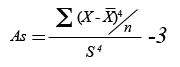 |
| Obtenció amb l’Excel | “Insertar”, “Función” i “CURTOSIS”. |