Dades estadístiques
Unitat 1. Conceptes estadístics bàsics
1. Definició d’estadística
En molts manuals sobre estadística hi podem trobar definicions de l’estadística, totes perfectament vàlides i que poden diferir en l’accent que poden posar els autors en un aspecte o un altre de la disciplina. Nosaltres proposem una definició que, sense pretendre que sigui original, creiem que incorpora adequadament tots els trets fonamentals en què tots els autors poden estar d’acord.
Estadística
Conjunt de teories i tècniques que tenen com a objectiu l’organització, presentació, descripció i anàlisi d’un conjunt de dades obtingudes a partir de poblacions o de mostres que representen les poblacions estudiades.
D’aquesta definició podem extreure les característiques principals de l’estadística, en el sentit de considerar que una part del seu contingut es basa en teories desenvolupades en el si de les Matemàtiques, com ara les teories de la probabilitat o de la mesura, però sens dubte l’estadística té una vessant aplicada molt important, que és la que ens proporciona les tècniques adequades per aconseguir diferents objectius. Aquests objectius es poden centrar en dos aspectes diferents:
-
La mera organització d’un conjunt de dades per simplificar-ne l'anàlisi posterior.
-
La presentació de les característiques principals, mitjançant la representació gràfica o la descripció quantitativa d'aquestes característiques.
Finalment, l’estadística també ens proporciona proves que ens permeten analitzar les dades dins un procés metodològic més ampli d’aplicació del mètode científic per tractar d’obtenir informació amb vista a resoldre problemes de tipus teòric o pràctic.
2. Definició de població, mostra i individu
Ja en la definició anterior hem utilitzat una sèrie de termes o conceptes que, tot i que són d'ús quotidià, requereixen una definició més formal que n'acoti el significat.
Aquests conceptes són els següents:
-
Població
-
Mostra
-
Individu (registre)
-
Paràmetre
-
Estadístic
Població
Grup sencer de subjectes dels quals intentem obtenir informació. En un estudi o una anàlisi estadística, la població és el conjunt, habitualment de subjectes, del qual volem generalitzar els resultats obtinguts. En aquest sentit, la delimitació clara de la població de referència o d’interès de l’estudi (població diana) és un element clau a l’hora de definir l’abast de les conclusions.
Mostra
Part de la població que estudiem amb l’objectiu d’obtenir informació.
En els estudis en què apliquem l’estadística habitualment treballem amb mostres de subjectes o casos, ja sigui per descriure determinades variables d’interès dels subjectes o per tractar d’inferir-ne els valors a escala poblacional. En aquest últim cas, la mostra ha de ser representativa de la població. Les tècniques de mostreig intenten aconseguir l’objectiu d’obtenir mostres representatives.
Individu (registre)
Element de la mostra o de la població. Persona, cas o objecte que conté informació que es vol estudiar.
new_pdf_page
Paràmetre
Propietat descriptiva d’una població. És, per tant, un valor numèric que ens resumeix alguna característica d’aquesta població.
Així, la mitjana d’edat dels habitants de Barcelona, si fos la població del nostre estudi, seria un paràmetre. Els paràmetres se simbolitzen mitjançant lletres gregues, i generalment són desconeguts.
Estadístic
Propietat descriptiva d’una mostra. O sigui, un valor numèric que ens informa d’alguna característica d’una mostra.
En el cas anterior dels habitants de Barcelona, si escollíssim una mostra d’aquests habitants i en calculéssim la mitjana d’edat, el valor obtingut seria un estadístic. Els estadístics se simbolitzen mitjançant lletres llatines.
Així, si volem fer un estudi sobre la població de la comarca del Maresme i seleccionem aleatòriament 1.500 habitants, la nostra població de referència són tots els habitants de la comarca del Maresme, mentre que la mostra són els 1.500 habitants seleccionats, i en què cada un és un individu del nostre estudi. Si en aquesta mostra calculéssim la proporció de població estrangera, aquest valor seria un estadístic, i si a partir de les dades oficials de tots els habitants de la comarca poguéssim obtenir la proporció de població estrangera de tota la comarca, aquest valor seria un paràmetre poblacional.
3. Definició de variable i tipus: qualitatives i quantitatives
En estadística, estudiem i analitzem variables com ara el sexe, la nacionalitat o l’edat dels individus en el cas de l’exemple que hem vist en l’apartat anterior. Segons les característiques que a escala estadística tinguin aquestes variables, la seva descripció i anàlisi es podrà dur a terme amb unes tècniques o unes altres. Per tant, en primer lloc, és important definir clarament què entenem per variable i sobretot tenir clars els criteris de classificació per aplicar-hi els procediments d’anàlisi adequats.
Variable
Qualsevol característica, com a propietat dels elements d’una població o mostra, que es pot manifestar en dues o més modalitats (variants). Per exemple, edat, sexe, opinió sobre una qüestió determinada, etc.
A escala estadística podem diferenciar o classificar les variables en dos tipus diferents:
-
Variables qualitatives (o categòriques): són les característiques que només es poden manifestar mitjançant categories considerades qualitats o atributs. Per exemple, sexe, lloc de residència, etc. En aquest tipus de variables, les modalitats són categories.
-
Variables quantitatives: són les característiques que es poden manifestar i mesurar mitjançant un nombre real. Les modalitats corresponen a nombres reals. Dins d’aquestes variables cal diferenciar entre:
-
Variables quantitatives discretes: els valors que poden presentar només són nombres aïllats. Per tant, entre dos valors consecutius no admeten valors intermedis. Per exemple, nombre de fills.
-
Variables quantitatives contínues: poden presentar valors infinits entre dos valors consecutius. Per exemple, edat, alçada, etc. Les variables contínues, per raons de precisió dels instruments de mesura, es poden considerar a la pràctica variables discretes. De totes maneres, per calcular alguns estadístics és convenient, en alguns casos, diferenciar entre el valor aparent i els límits reals d’aquest valor. Així, el valor aparent 50 (per exemple, una edat de 50 anys) és en realitat un interval entre els valors reals 49,5 i 50,5.
-
4. Escales de mesura
Quan assignem valors numèrics a cada una de les modalitats d'una variable estem generant una escala de mesura. Aquest procés s'aplica d'acord amb unes regles establertes, de les quals s'ocupa la teoria de la mesura.
Dit més formalment, una escala de mesura és un procediment mitjançant el qual es relacionen biunívocament un conjunt de modalitats diferents amb un conjunt de nombres diferents, és a dir, a cada modalitat li correspon un únic nombre, i a cada nombre, una única modalitat.
Així, si assignem un 1 a la modalitat “Gens satisfet” com a resposta a la pregunta sobre satisfacció en els serveis d’una biblioteca pública, un 2 a la resposta “Ni molt ni poc satisfet” i un 3 a la resposta “Molt satisfet”, estem generant una escala de mesura per valorar el grau de satisfacció dels usuaris.
En funció de les relacions que podem comprovar empíricament entre els valors numèrics assignats a les modalitats de l'escala, i els tipus de transformacions que podem fer d’aquests valors, podem distingir quatre tipus d’escales de mesura:
-
Nominals
-
Ordinals
-
D’interval
-
De raó
Escala nominal
L’escala nominal és aquella en la qual només es pot comprovar empíricament si les modalitats són iguals o diferents (relació d’igualtat o de desigualtat). Les transformacions possibles poden ser qualssevol, ja que els nombres o valors numèrics assignats a les modalitats són meres etiquetes de les modalitats o categories.
Per exemple, el municipi de residència d’un grup d’usuaris. Així, podem assignar un 1 als usuaris de Barcelona, un 2 als de Badalona, etc., però també podríem assignar l’1 als de Badalona, el 2 als de Barcelona, etc.
Els nombres no tenen propietats matemàtiques, i en aquest sentit no admeten operacions aritmètiques (suma, resta, etc.).
Escala ordinal
En les escales ordinals, a més de poder comprovar si les modalitats són iguals o diferents, podem saber quines són més grans o prèvies a les altres en cas que siguin diferents. Per tant, els nombres assignats a les diferents modalitats admeten les relacions d’igualtat o de desigualtat i d’ordre. Les transformacions possibles són totes les que mantinguin l’ordenació original.
Per exemple, la numeració dels edificis d’un carrer o l’escala de duresa dels materials.
Els nombres només tenen la propietat matemàtica de la seva ordenació, però tampoc no admeten operacions aritmètiques, ja que no hi ha una mateixa quantitat de modalitat entre valors consecutius de l’escala.
Escala d’interval
En les escales d’interval, a més de poder comprovar empíricament la igualtat o desigualtat i l’ordre, també s’estableix una unitat empírica de mesura que ens permet determinar la distància entre dues modalitats qualssevol. El valor nul de l’escala és designat per convenció (arbitrari).
Les transformacions possibles són les lineals que s’expressen segons l'equació:
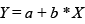
A on X i Y són els diferents valors de les dues escales (la original i la transformada).
Per exemple, l’escala de temperatura, on hi ha una unitat (el grau de temperatura), però el valor 0 es pot situar en diferents punts. Així, en l’escala centígrada o Celsius, el valor de 0 se situa en el punt de congelació de l’aigua, mentre que en l’escala Fahrenheit el 0 se situa en una temperatura més baixa (concretament 31,75 graus centígrads més avall). Pel que fa a les transformacions entre les dues escales de temperatura, si X és el valor en l’escala centígrada i Y el valor corresponent en l’escala Fahrenheit, l’equació lineal que ens permet transformar els graus centígrads en Fahrenheit és la següent: Y = 31,75 + 1,79 X. Els nombres atribuïts a les modalitats mantenen propietats matemàtiques de distància entre valors, d'aquesta manera hi ha la mateixa diferència de temperatura entre 5 i 10 graus centígrads que entre 20 i 25 graus, però no les de raó, perquè les proporcions no es mantenen constants i, per tant, 20 graus no és el doble de temperatura de 10 graus.
Escala de raó
En l’escala de raó, a més de permetre verificar empíricament totes les relacions de les escales anteriors, hi ha un valor nul (no arbitrari) que indica l’absència de la característica que s'ha de mesurar.
Les transformacions possibles són un subconjunt de les lineals on:
![]()
Per exemple, la longitud o el nombre d’usuaris. Així, la longitud la podem mesurar en metres o en peus o en altres unitats, i la transformació d’una en l’altra tan sols requereix conèixer l’equivalent d’una unitat en l’altra. En aquesta última escala de mesura, els nombres atribuïts a les modalitats mantenen totes les propietats matemàtiques, tant de distància entre valors com de proporcions entre ells. D'aquesta manera, hi ha la mateixa distància entre 5 i 10 metres que entre 15 i 20. A més, 20 metres és el doble de distància que 10.
Aquesta tipificació de les escales de mesura es pot relacionar amb la classificació de les variables vista en l’apartat anterior de la manera següent:
-
Les variables qualitatives es poden mesurar en escales nominals (les més habituals) o ordinals.
-
Les variables quantitatives es poden mesurar en escales ordinals, d’interval o de raó (les més habituals).