Dades estadístiques

Fitxes resum

Conceptes bàsics

Estadística Conjunt de teories i tècniques que tenen com a objectiu l’organització, la presentació, la descripció i l'anàlisi d’un conjunt de dades obtingudes a partir de poblacions o de mostres que representen les poblacions estudiades.
Població Grup sencer de subjectes dels quals intentem obtenir informació.
Mostra Part de la població que estudiem amb l’objectiu d’obtenir-ne informació.
Individu (registre) Element de la mostra o de la població. Persona, cas o objecte que conté informació que es vol estudiar.
Paràmetre Propietat descriptiva d’una població. És, per tant, un valor numèric que resumeix alguna característica de la mateixa població.
Estadístic Propietat descriptiva d’una mostra. O sigui, un valor numèric que ens informa d’alguna característica d’una mostra.
Variable Qualsevol característica, com a propietat dels elements d’una població o mostra, que es pot manifestar en dues o més modalitats (variants). Per exemple: edat, sexe, opinió sobre una qüestió determinada, etc.
Variables qualitatives Són les característiques que només es poden manifestar mitjançant categories considerades qualitats o atributs. Per exemple: sexe, lloc de residència, etc. Les modalitats són categories.
Variables quantitatives Són les característiques que es poden manifestar i mesurar mitjançant un nombre real. Les modalitats corresponen a nombres reals.
Variables quantitatives discretes Els valors que poden presentar només són nombres aïllats. Per tant, entre dos valors consecutius no admeten valors intermedis. Per exemple: nombre de fills.
Variables quantitatives contínues Poden presentar valors infinits entre dos valors consecutius. Per exemple: edat, alçada.

Descripció d’una variable qualitativa

Taula de freqüències

Les taules de freqüències ens proporcionen informació sobre els diferents valors, modalitats o categories de la variable i el recompte absolut o relatiu del nombre de casos de cada categoria.

Exemple 1:

Sexe fi pi Pi
1: Home 527 0,504 50,4
2: Dona 519 0,496 49,6
Total 1046 1 100
  • fi = Freqüència absoluta: recompte del nombre de casos de cada categoria de la variable en la mostra estudiada.
  • Obtenció amb l’Excel: programa preconfigurat de “Análisis de datos”: “Histograma”.
  • Freqüència relativa en proporcions (pi): Proporció, o sigui tant per u, del nombre de casos (subjectes) de cada categoria sobre el total de la mostra. S’obté dividint la freqüència absoluta de cada categoria pel total de casos o subjectes:
Fórmula
Per als homes de l'exemple
  • Freqüència relativa en percentatges (Pi): percentatge, o sigui tant per cent, del nombre de casos (subjectes) de cada categoria sobre el total de la mostra. S’obté dividint la freqüència absoluta de cada categoria pel total de casos o subjectes, i multiplicant el resultat per cent:
Fórmula
Per als homes de l'exemple

Exemple 2:

Edat fi pi Pi fa pa Pa
1: Menors de 16 185 0,177 18 185 0,177 18
2: Entre 16 i 64 702 0,671 67 887 0,848 85
3: Majors de 64 159 0,152 15 1046 1 100
Total 1046 1 100
  • Freqüència absoluta acumulada (fa): recompte del nombre de casos (subjectes) que pertanyen a cada categoria o a categories inferiors. S’obté sumant la freqüència absoluta d’una categoria amb les de les categories que són inferiors a aquesta mateixa categoria.
  • Freqüència relativa acumulada en proporcions (pa): proporció, o sigui tant per u, del nombre de casos (subjectes) de cada categoria o de categories inferiors sobre el total de la mostra. S’obté dividint la freqüència acumulada absoluta de cada categoria pel total de casos o subjectes:
Fórmula
Per als subjectes d'entre 16 i 64 anys de l'exemple 2
  • Freqüència relativa acumulada en percentatges (Pa): percentatge, o sigui tant per cent, del nombre de casos (subjectes) de cada categoria o de categories inferiors sobre el total de la mostra. S’obté dividint la freqüència absoluta acumulada de cada categoria pel total de casos o subjectes, i multiplicant el resultat per cent:
Fórmula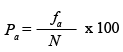
Per als subjectes d'entre 16 i 64 anys de l'exemple 2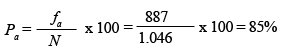

Representacions gràfiques

Diagrama de barres

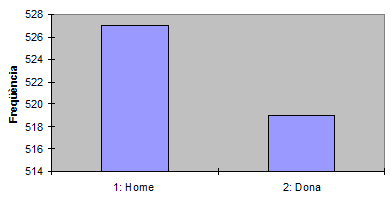
  • Obtenció amb l’Excel: programa preconfigurat de “Análisis de datos”, “Histograma”.

Ciclograma

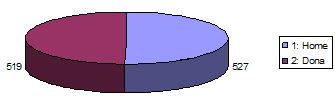
  • Obtenció amb l’Excel: “Insertar”, “Gráfico” i “Circular”.

Descripció d’una variable quantitativa

Taula de freqüències agrupades per intervals o classes

Exemple:

Edat fi pi Pi fa pa Pa
de 1 a 15 anys 185 0,177 18 185 0,18 18
de 16 a 30 anys 169 0,162 16 354 0,34 34
de 31 a 45 anys 254 0,243 24 608 0,58 58
de 46 a 60 anys 211 0,202 20 819 0,78 78
de 61 a 75 anys 158 0,151 15 977 0,93 93
majors de 75 anys 69 0,066 7 1046 1 100
Total 1046 1 100
  • Obtenció amb l’Excel: programa preconfigurat de “Análisis de datos”, “Histograma”.

Representacions gràfiques

Histograma

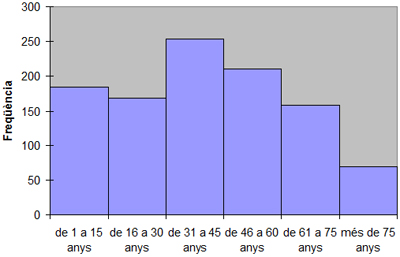
  • Obtenció amb l’Excel: programa preconfigurat de “Análisis de datos”, “Histograma”.

Polígon de freqüències

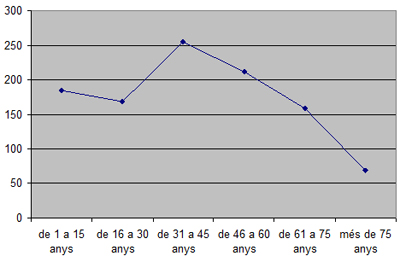
  • Obtenció amb l’Excel: “Insertar”, “Gráfico” i “Líneas”.

Indicadors descriptius

Tendència central (Centralitat)

Mitjana aritmètica o mitjana

()

Definició Sumatori de totes les dades de la distribució dividit pel nombre de dades.
Ús i interpretació Indicador més àmpliament utilitzat. Menys representatiu en cas que la distribució sigui força asimètrica.
Fórmula
Obtenció amb l’Excel “Insertar”, “Función” i “PROMEDIO”.

Mediana (Md)

Definició Valor de la distribució que, un cop ordenades les dades de menor a major, deixa un 50% de dades per sota i l’altre 50% per sobre.
Ús i interpretació Indicat si la variable s'ha mesurat amb escala ordinal. Més representatiu que la mitjana si la distribució és força asimètrica.
Fórmula Buscar el valor de la distribució que ocupa la posició , en què “n” és el nombre total de subjectes o casos.
Obtenció amb l’Excel “Insertar”, “Función” i “MEDIANA”.

Moda (Mo)

Definició Valor més freqüent d’una distribució de dades.
Ús i interpretació Útil per a variables qualitatives i en cas que busquem perfils prototípics.
Obtenció amb l’Excel “Insertar”, “Función” i “MODA”.

new_pdf_page

Variabilitat o dispersió

Variància

(S2)

Definició Sumatori de les puntuacions de desviació al quadrat dividit pel nombre de valors menys un.
Ús i interpretació Menys utilitzat que la desviació típica, ja que les unitats que la componen són les pròpies de la variable al quadrat
Fórmula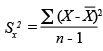
Obtenció amb l’Excel “Insertar”, “Función” i “VAR”.

Desviació típica o desviació estàndard (S)

Definició Arrel quadrada de la variància.
Ús i interpretació Indicador de dispersió més utilitzat, ja que les unitats que la componen són les pròpies de la variable.
Fórmula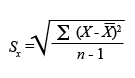
Obtenció amb l’Excel “Insertar”, “Función” i “DESVEST”.

Coeficient de variació (CV)

Definició Percentatge de variació respecte a la mitjana de la distribució.
Ús i interpretació Indicador de dispersió utilitzat per comparar variabilitats de diferents variables, o de la mateixa variable en mostres amb mitjana diferent.
Fórmula

new_pdf_page

Ordre o posició

Percentil

(Pk)

Definició Valor de la distribució de dades que, un cop ordenades de menor a major, deixen un percentatge (k) determinat de casos o subjectes per sota.
Ús i interpretació Útil a l'hora de buscar el valor de la distribució que deixa un percentatge determinat de casos per sota o per sobre.
Fórmula Pk: buscar el valor de la distribució que ocupa la posició, en què “n” és el nombre total de subjectes o casos i «k», el percentil que busquem (de 1 a 100).
Obtenció amb l’Excel “Insertar”, “Función” i “PERCENTIL”.

Quartils (Q)

Definició Si els percentils divideixen la distribució en cent parts iguals, el quartils ho fan en quatre.
Ús i interpretació Igual que els percentils, però deixant un 25, 50 o 75% de casos per sota.
Fórmula Qk: buscar el valor de la distribució que ocupa la posició, en què “n” és el nombre total de subjectes o casos i «k», el quartil que busquem (d'1 a 4).
Obtenció amb l’Excel “Insertar”, “Función” i “CUARTIL”.

new_pdf_page

Forma

Coeficient d'asimetria (As)

Definició Distribució dels valors a una banda i a l'altra de la mitjana.
Ús i interpretació Útil per estudiar la simetria o asimetria (positiva o negativa) de la distribució i per decidir, en alguns casos, quin serà l'indicador de tendència central més representatiu.
Fórmula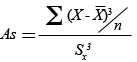
Obtenció amb l’Excel “Insertar”, “Función” i “COEFICIENTE.ASIMETRIA”.

Curtosi o apuntament (Cr)

Definició Concentració de valors propers a la mitjana.
Ús i interpretació Només és interpretable si la distribució és simètrica i ens permet determinar si és aplanada, normal o apuntada.
Fórmula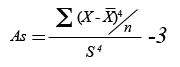
Obtenció amb l’Excel “Insertar”, “Función” i “CURTOSIS”.
Pujar