Si volem obtenir la taula de freqüències del sexe de la mostra de 1.046 subjectes de la matriu de dades “dades_alt_penedes”, la millor alternativa amb l’Excel és utilitzar l’opció de “Histograma” dins els programes preconfigurats d’anàlisi de dades.
A continuació, farem una activitat pas a pas per posar en pràctica les taules de freqüència.
Aquesta activitat consisteix a seguir unes indicacions pas a pas a fi d'obtenir la taula de freqüències del sexe de la mostra anterior. Per poder-ho fer, us heu de descarregar el següent document.
Un cop hàgiu seguit els passos anteriors i aplicat les modificacions a la matriu, la taula de freqüències definitiva i el gràfic corresponent que obtindreu seran els següents:
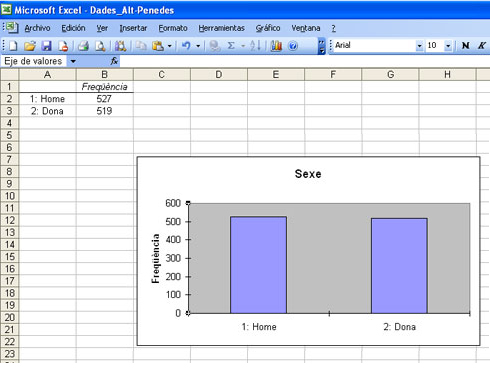
Un cop hem obtingut el resultat, ja podem copiar en qualsevol document tant la taula de freqüències com el diagrama de barres.
pi = Freqüència relativa en proporcions
Proporció, o sigui tant per u, del nombre de casos (subjectes) de cada categoria sobre el total de la mostra.
La freqüència relativa en proporcions s’obté dividint la freqüència absoluta de cada categoria pel total de casos o subjectes. El sumatori total d’aquestes freqüències ha de ser igual a 1.
pi = Freqüència relativa en proporcions
En l'exemple, calcularíem la proporció d’homes de la manera següent:
Pi = Freqüència relativa en percentatges
Percentatge, o sigui tant per cent, del nombre de casos (subjectes) de cada categoria sobre el total de la mostra.
S’obté dividint la freqüència absoluta de cada categoria pel total de casos o subjectes, i multiplicant el resultat per cent. El sumatori total d’aquestes freqüències ha de ser igual a 100.
Pi = Freqüència relativa en percentatges
En l'exemple, calcularíem el percentatge d’homes de la manera següent:
La taula de freqüències amb les freqüències absolutes i relatives i els sumatoris de cada una seran els següents:
| Sexe | fi | pi | Pi |
|---|---|---|---|
| 1: Home | 527 | 0,504 | 50,4 |
| 2: Dona | 519 | 0,496 | 49,6 |
| Total | 1046 | 1 | 100 |
Les freqüències relatives seran més útils que les absolutes quan vulguem comparar una mateixa variable obtinguda en mostres de diferents mides. Així, podríem comparar les dades anteriors amb les d’una mostra d’habitants d’alguna altra comarca en què la quantitat fos diferent dels 1.046 de la nostra mostra.
Si la variable qualitativa que descrivim està mesurada en una escala ordinal, a més de les freqüències anteriors, absolutes o relatives, també podem obtenir les freqüències acumulades per cada categoria, que ens informaran del nombre de casos o subjectes d’un nivell igual o inferior a una categoria determinada.
Així, en l'exemple podem obtenir les freqüències acumulades per la variable “Edat-2” que hem categoritzat a partir de l’edat dels subjectes. Les instruccions per obtenir la taula de freqüències absolutes amb l’Excel seguiran el mateix format que per conèixer la variable “sexe”, únicament cal tenir en compte que en aquest cas el nombre de categories de la variable és de tres en lloc de les dues de la variable «sexe».
La taula de freqüències d’aquesta variable, amb les absolutes, relatives i acumulades, serà la següent:
| Edat | fi | pi | Pi | fa | pa | Pa |
|---|---|---|---|---|---|---|
| 1: Menors de 16 | 185 | 0,177 | 18 | 185 | 0,177 | 18 |
| 2: Entre 16 i 64 | 702 | 0,671 | 67 | 887 | 0,848 | 85 |
| 3: Majors de 64 | 159 | 0,152 | 15 | 1046 | 1 | 100 |
| Total | 1046 | 1 | 100 |
En aquesta taula de freqüències hem obtingut, a més de les freqüències absolutes i relatives comentades anteriorment, les freqüències acumulades també absolutes o relatives, que són:
fa = Freqüència absoluta acumulada
Recompte del nombre de casos (subjectes) que pertanyen a cada categoria o a categories inferiors.
La freqüència absoluta acumulada s’obté sumant la freqüència absoluta d’una categoria amb les de les categories inferiors. La freqüència absoluta acumulada fins a l'última categoria ha de ser igual al nombre total de casos o subjectes de la mostra.
pa = Freqüència relativa acumulada en proporcions
Proporció, o sigui tant per u, del nombre de casos (subjectes) de cada categoria o de categories inferiors sobre el total de la mostra.
La freqüència relativa acumulada en proporcions s’obté dividint la freqüència acumulada absoluta de cada categoria pel total de casos o subjectes. La freqüència relativa acumulada en proporcions per l'última categoria ha de ser igual a 1.
pa = Freqüència relativa acumulada en proporcions
En l'exemple, els subjectes entre 16 i 64 anys es calcularien de la manera següent:
Pa = Freqüència relativa acumulada en percentatges
Percentatge, o sigui tant per cent, del nombre de casos (subjectes) de cada categoria o de categories inferiors sobre el total de la mostra.
La frqüència relativa acumulada en percentatges s’obté dividint la freqüència absoluta acumulada de cada categoria pel total de casos o subjectes, i multiplicant el resultat per cent. La freqüència relativa acumulada en percentatges per l'última categoria ha de ser igual a 100.
Pa = Freqüència relativa acumulada en percentatges
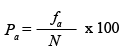
En l'exemple, calcularíem els subjectes entre 16 i 64 anys de la manera següent:
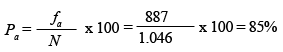
Les freqüències acumulades ens permeten obtenir informació sobre el total o el percentatge de casos, per sobre o per sota d’una determinada categoria.
Així, en l'exemple, podem observar que el 85% dels habitants del Baix Penedès tenen una edat inferior als 65 anys. Com que també es tracta d'una freqüència relativa, ens podria servir per fer una anàlisi comparativa de l’edat dels habitants d’aquesta comarca amb la d’una altra mostra d’habitants d’una comarca diferent, encara que aquesta altra mostra no tingués la mateixa mida que la nostra.
Evidentment, si la variable qualitativa que analitzem no s'hagués mesurat en una escala ordinal, les freqüències acumulades no tindrien cap sentit, ja que l'ordenació de les categories de la variable no seria natural.
A partir de la taula que hem elaborat a l'apartat sobre freqüències acumulades, podríem representar el diagrama de barres amb les freqüències acumulades absolutes o relatives d’una variable qualitativa mesurada amb una escala ordinal. Així, per representar el mateix exemple anterior de la variable “Edat-2”, en forma de diagrama de barres amb els percentatges acumulats, ho faríem de la manera següent:
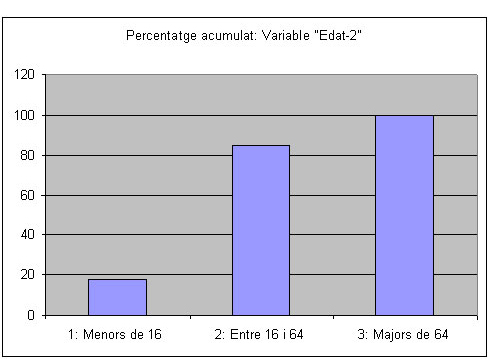
Per dissenyar el diagrama de barres acumulat amb l’Excel podem utilitzar el gràfic de “Columnas”.
En aquesta activitat, us proposem que feu el diagrama anterior seguint un procés pas a pas. Per fer-ho, us heu de descarregar el següent document.
L’altra representació gràfica que s'utilitza molt sovint per representar els valors d’una variable qualitativa és el ciclograma o diagrama de sectors.
Els passos que cal seguir per dibuixar un ciclograma són els següents:
-
Dibuixem una circumferència.
-
Dins la circumferència, repartim una porció d’àrea per cada categoria que sigui proporcional a la freqüència absoluta (o relativa) d’aquella categoria.
En aquesta activitat, us proposem que feu el ciclograma anterior seguint un procés pas a pas. Per fer-ho, us heu de descarregar el següent document.