Investigació d’accidents de circulació
4. Física del moviment
4.1. Conceptes fonamentals
4.1.1. Energia cinètica i principi de la conservació d’energia
La magnitud d’energia cinètica, que és la que posseeix un mòbil en virtut del seu moviment, és una dimensió escalar que depèn de la massa i la velocitat del mòbil.
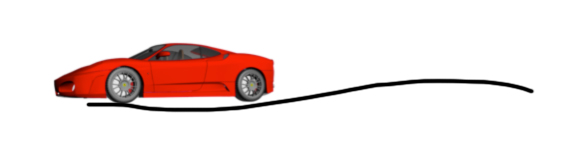
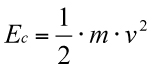
Sobre la base del principi de la conservació d’energia, perquè es produeixi l’aturada d’un vehicle la seva energia cinètica (Ec) s’haurà de transferir i ser desenvolupada en un altre tipus d’energia.
Recordem que l’energia no es pot crear ni destruir, encara que una forma d’energia sí que es pot transformar en una altra. Així, es compleix: Energia cinètica = energia1 + energia2 + energian
4.1.2. El concepte d’adherència en la interacció via-vehicle
Si partim de la premissa que un accident és un esdeveniment inesperat, hem de considerar que la resposta del conductor implicat ha de ser similar a la de qualsevol altra persona que no hi estigui relacionada; davant d’una situació de risc imminent la reacció és accionar els frens per aturar el vehicle.
Si no l’ha pogut aturar dins de l’àrea de percepció, s’ha determinar per què. Per tant, és necessari que l’investigador o investigadora posseeixi els coneixements necessaris per donar resposta a aquest interrogant.
A més de l’impuls subministrat pel motor al seu eix de tracció, perquè un vehicle pugui partir de la seva posició de repòs necessitem una força d’adherència exercida pels pneumàtics amb la calçada, tant per disposar de motricitat (adherència longitudinal), com per disposar de capacitat de gir (adherència transversal).
Aquesta força és proporcional a la força normal (Fn) que pressiona els pneumàtics contra la superfície de la calçada i al coeficient d’adherència (µ), que sorgeix dels enllaços que exerceixen entre si les molècules de les dues superfícies en contacte, la magnitud del qual depèn de la seva.

En què
m = massa del vehicle
µ = coeficient d’adherència
g = acceleració de la gravetat terrestre, 9.81 m/s²
Respecte a la via, el valor d’aquest coeficient està determinat per la naturalesa i l’estat del paviment a causa de les condicions meteorològiques i circumstancials (pluja, neu, gel, oli, graveta, fulles seques…), les quals fan que el seu valor disminueixi.
Respecte al vehicle, el valor de l’adherència està determinat fonamentalment per l’estat dels pneumàtics, la seva composició i el grau de pressió.
A més dels anteriors hem de considerar altres factors, com l’estat de la suspensió del vehicle o la velocitat.
La taula següent, publicada pel Servei Català de Trànsit, reflecteix els coeficients d’adherència dinàmics obtinguts amb bloqueig de roda de vehicles de la classe turisme pel Traffic Institute de la Universitat de Northwestern:
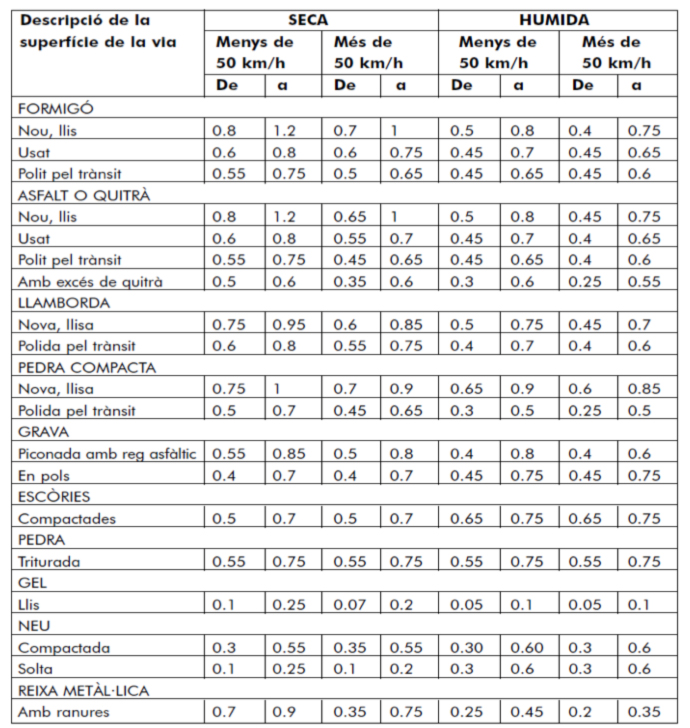
Experimentalment s’ha observat que l’adherència aconsegueix el seu valor màxim quan el percentatge de fregament del pneumàtic està situat entre el 10 i el 30%, corresponent al coeficient de fregament estàtic, situació en la qual treballa el sistema de frens antibloqueig (ABS).
4.2. Càlcul de la velocitat basat en les empremtes de frenada
En cas d’una frenada d’emergència, en què l’energia cinètica es transforma en energia calorífica generada al llarg de la distància de frenada, es compleix la igualtat següent:
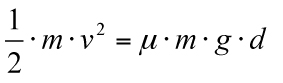
En què
µ = coeficient d’adherència
m = massa del vehicle
g = acceleració de la gravetat terrestre, 9.81 m/s²
d = distància de frenada
v = velocitat del vehicle
En desenvolupar el sistema d’equacions obtenim una variant de l’expressió principal del moviment uniformement accelerat, el resultat de la qual ofereix la velocitat del vehicle determinat en m/s.
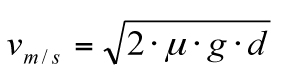
Cas pràctic 1
Un turisme circula pel carrer Diputació de Barcelona. Uns metres abans d’arribar a un pas de vianants, el/la conductor/a frena per la presència d’una persona que comença a travessar la via. Durant la seva aturada el vehicle deixa 12 metres d’empremtes de frenada. Calcula la velocitat de circulació del vehicle, si el valor del coeficient de fregament del pneumàtics és de 0,70.

La unitat generalment utilitzada per expressar la velocitat dels vehicles és el
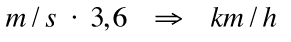
km/h, així que haurem de fer la conversió:
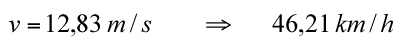
4.2.1. Correcció del coeficient d’adherència a causa del desnivell
Quan la calçada no està a nivell i presenta un cert angle d’inclinació (ϴ) és necessari tenir en compte la component de la força de gravetat a conseqüència del pes del vehicle, per la qual cosa haurem d’introduir a les equacions un factor de correcció del coeficient de fregament.
μ corregit = μ cos θ ± sin θ
La raó trigonomètrica sinus (sin) adopta el signe positiu quan la calçada presenta una inclinació ascendent (rampa), i negatiu en pendent.
A la pràctica, quan el desnivell no és gaire pronunciat, la correcció del coeficient de fregament pren el valor de la tangent de l’angle.
μ corregit = μ± tang θ
Aquest factor de correcció adopta el signe de l’equació en les mateixes condicions exposades abans.
Cas pràctic 2
Un vehicle circula per una via el pendent de la qual és el que reflecteix la figura. Després que el/la conductor/a faci una frenada d’emergència s’observen a la calçada 12 metres de petjades de frenada. Calcula la velocitat de circulació del vehicle si el coeficient de fregament és de 0,70.

Factor de correcció:

Velocitat de circulació del vehicle:

4.2.2. Les fases del procés de frenada
Les empremtes de frenada no apareixen de manera immediata en accionar el sistema de frenada.
En una primera fase, des que el/la conductor/a acciona el pedal de fre fins que es produeix el bloqueig de les rodes transcorre un període de temps que està determinat directament per l’eficàcia del sistema de frenada, que anomenem temps de resposta mecànica dels elements de fre.
Durant aquest interval de temps la desacceleració del vehicle passa d’un valor zero a un valor màxim, que està directament relacionat amb el coeficient de fregament.
Alguns assajos fets amb frens en bon estat han mostrat que el temps de resposta mecànica per a turismes és de l’ordre de 0,20 segons.
D’altra banda, regulat per directiva europea (Directiva de la Comissió, de 23 de desembre de 1985, per la qual s’adapta al progrés tècnic la Directiva del Consell 71/320/CEE, sobre els dispositius de frenada) s’estableix un temps màxim perquè la força de frenada aconsegueixi l’eficàcia mínima requerida de 0,6 segons.
En produir-se el bloqueig de les rodes, començaran a lliscar sobre el paviment. Una vegada que l’escalfor generada per totes dues superfícies en contacte, pneumàtic i paviment, aconsegueixi la temperatura de fusió de la banda de rodament apareixeran les petjades de frenada.
Diversos estudis sobre aquest procés determinen que l’espai recorregut sense l’aparició de marques pot oscil·lar entre un i quatre metres.
Del que s’ha exposat anteriorment es desprèn que la velocitat obtinguda a partir de l’anàlisi de les empremtes serà inferior a la velocitat real de circulació.
Amb la finalitat d’obtenir un valor més precís ha estat acceptat un model matemàtic que es fonamenta en el concepte físic del moviment accelerat uniformement, el qual considera la desacceleració soferta durant el temps de resposta mecànica dels frens.
Si l’acceleració és constant, la velocitat varia linealment en el temps; per tant es compleix que:

Com que la desacceleració del vehicle passa d’un valor zero a un valor màxim durant el temps de resposta mecànica, n’hem d’obtenir el valor mitjà:

Hi ha una relació directa entre la desacceleració i el coeficient de fregament:
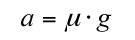
Per tant, l’expressió final resultant és:
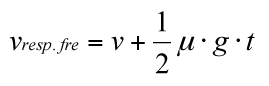
En què
vresp. fre = velocitat en accionar el fre del vehicle
v = velocitat a l’inici de les empremtes de frenada
µ = coeficient d’adherència
g = acceleració de la gravetat terrestre 9.81 m/s²
t = temps de resposta del fre
Cas pràctic 3
El vehicle de l’exercici 1, a l’inici de les empremtes de frenada, circulava a una velocitat de 12,83 m/s - 46,21 km/h. Calcula’n la velocitat de circulació si considerem que el temps de resposta mecànica dels sistema de fre està comprès entre 0,2 i 0,6 segons.
a) Temps de resposta mecànica del fre: 0,2 segons

b) Temps de resposta mecànica del fre: 0,6 segons
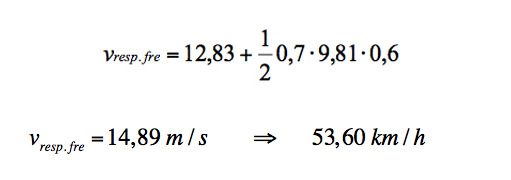
4.3. Accidents amb vehicles de dues rodes
L’auge dels vehicles de dues rodes com a mitjà de transport en el desplaçament dins de les grans ciutats ha incidit negativament en la sinistralitat del sector, com confirmen els estudis que ha efectuat la DGT els darrers anys.
És necessari, per aquest motiu, que l’agent de la policia local encarregat de les tasques d’investigació posseeixi la formació específica que li permeti reconèixer les diferents forces que actuen sobre aquest segment de vehicles durant un accident.
4.3.1. Desacceleració i coeficient de fregament dels pneumàtics
Un punt clau a l’hora de determinar la velocitat d’una motocicleta que ha deixat marcades les empremtes de frenada és poder concretar quin fre s’ha utilitzat, ja que això està directament relacionat amb la desacceleració del vehicle.
Gràficament, la imatge següent representa la distància d’aturada en funció del fre accionat.
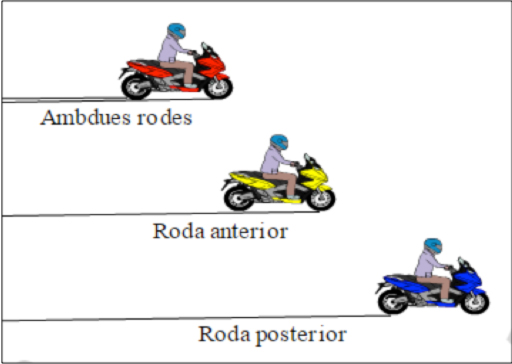
Un procediment que pot utilitzar l’agent de policia és basa en l’examen de la banda de rodament dels pneumàtics, en què detectarà una zona de color més intens, que serà la que ha lliscat sobre la calçada mentre la roda estava bloquejada.
Un segon mètode consisteix en l’anàlisi de l’amplada de les empremtes de pneumàtic impreses a la calçada.
Un exemple el veiem en els resultats obtinguts per DEKRA als assajos de frenada fets amb una motocicleta de la marca Suzuki, model GSX-R 750. Durant les proves es va veure que el pneumàtic de la roda anterior va deixar impresa una empremta de 140-150 mm d’ample, mentre que la marcada pel pneumàtic de la roda posterior va ser només d’una amplada de 60-90 mm.
Això es produeix per la transferència de pes cap al davant que es produeix quan accionem el fre davanter del vehicle, que comporta l’aplanament del pneumàtic de l’eix anterior.
El manual d’investigació d’accident del Servei Català de Trànsit, a partir de les proves fetes pels investigadors Frick, Ryley i Warner, recull el valors indicats a la taula adjunta, que corresponen a la desacceleració que experimenten aquest tipus de vehicles durant la frenada.
| Roda bloquejada | Coeficient | Desacceleració |
| Totes dues rodes | 0.80 - 0.92 | 8.5 (±) 0,6 |
| Anterior | 0.60 - 0.70 | 6.4 (±) 0,5 |
| Posterior | 0.30 - 0.40 | 3.5 (±) 0,5 |
4.3.2. Coeficient d’arrossegament lateral
És típic en els accidents de motocicletes i ciclomotors que després de la fase de frenada es produeixi la seva caiguda i el lliscament posterior sobre un dels seus laterals. Durant aquest desplaçament s’origina una desacceleració a causa de les forces de fregament que interactuen entre els elements protuberants del vehicle i el paviment.
Una classificació a efectes orientatius del coeficient d’adherència, que com hem vist té una relació directa amb la desacceleració, és la representada al quadre adjunt, estructurat d’acord amb el factor velocitat.
| Km/h | ||||
| Asfalt | 16 - 30 | 40 - 50 | 60 - 80 | 80 - 90 |
| Coeficient | 0.66 - 0.57 | 0.59 - 0.45 | 0.43 - 0.38 | 0.36 - 0.33 |
Els coeficients d’adherència resultant durant el lliscament dels vehicles amb carenat de fibra o tipus scooter tendeixen a ser inferiors en 0,10 punts.
Cas pràctic 4
Una patrulla de la policia local ha d’intervenir en la investigació d’un accident en què s’ha produït la caiguda d’un motorista en efectuar una frenada d’emergència.
Els agents fan un mesurament de:
-
5 metres d’empremtes d’arrossegament de la motocicleta sobre el seu lateral esquerre. S’estima un coeficient de fregament del seu lateral de 0.45.
-
12 metres d’empremtes de frenada, anteriors a la caiguda, que pertanyen a la roda del seu eix anterior. S’estima un coeficient de fregament de 0.65.
a) En sentit invers als fets succeïts, calcularem en primer ordre la velocitat que posseïa la motocicleta a l’inici de les empremtes d’arrossegament.
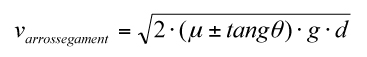
En què
µ = coeficient d’adherència, 0,45
g = acceleració de la gravetat terrestre, 9.81 m/s²
d = longitud d’empremtes d'arrossegament 5 m
Calçada a nivell, tang θ ± 0
En desenvolupar l’expressió amb les dades de l’accident obtenim un resultat de 6,64 m/s.
b) Amb la dada anterior, mitjançant una variant de l’expressió fonamental del moviment uniformement accelerat podrem obtenir la velocitat de la motocicleta a l’inici de les empremtes de frenada.
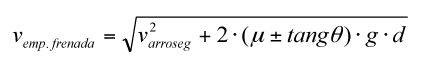
En què
µ = coeficient d’adherència, 0,65
g = acceleració de la gravetat terrestre, 9.81 m/s²
d = longitud d’empremtes de frenada, 12 m
Calçada a nivell, tang θ ± 0
El resultat de la qual determina que la velocitat de la motocicleta a l’inici de les empremtes de frenada era de 14,03 m/s; 50,54 km/h.
4.3.3. Mètode EBS
En un accident de trànsit part de l’energia cinètica que posseeixen els vehicles és transformada en energia de deformació.
Una manera d’avaluar aquesta energia consisteix a comparar els danys del vehicle accidentat amb les deformacions resultants d’assajos de xoc (crash-test) efectuats a una velocitat coneguda.
Quan una motocicleta sofreix un impacte frontal, al seu apartat mecànic la resultant sol ser una deformació de la forqueta davantera de suspensió i dels seus elements adjacents, eix, discos de fre i roda, com podem veure a la imatge següent: detall de la reculada de forqueta en un crash-test fet per DEKRA.

Les deformacions consistents en la reducció de la distància entre eixos d’aquest tipus de vehicles han estat estudiades i s’estableix empíricament la relació proporcional entre la velocitat d’impacte EBS i la profunditat de deformació resultant.

La gràfica anterior ha estat confeccionada sobre la base dels estudis duts a terme per Severy. Els assajos fets per l’investigador van consistir en el xoc de motocicletes de cilindrades compreses entre 90 i 750 cc contra el lateral de vehicles de la classe turisme.
4.4. Accidents en corba per excés de velocitat
4.4.1. Velocitat crítica en traçar una corba
La velocitat crítica d’una corba és aquella velocitat màxima a la qual un vehicle pot descriure el traçat de la via sense sortir en línia recta cap al seu exterior.
D’acord amb els principis fonamentals de la física, quan un vehicle traça una corba circular actua sobre ell una força centrípeta la magnitud de la qual depèn de la massa del vehicle, de la seva velocitat de circulació i del radi de la via, representat a la figura següent.

L’expressió física que representa la força centrípeta s’estableix com:

La velocitat màxima que manté el vehicle en la seva trajectòria circular sense que es produeixi el derrapatge està determinat pel límit d’adherència; és a dir, mentre la força centrípeta que dirigeix el vehicle cap a l’exterior de la corba no superi la força d’adherència que permet la seva capacitat de gir. Aquesta condició podem expressar-la mitjançant el sistema d’equacions:
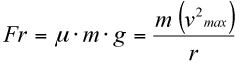
En què:
µ = coeficient d’adherència
m = massa del vehicle
r = radi de la corba
g = acceleració de la gravetat terrestre. 9,81 m/s2
v = velocitat crítica de la corba
En una via a nivell, la velocitat màxima a la qual podrà traçar el vehicle la corba ve donada per l’expressió:

En què:
µ = coeficient d’adherència
r = radi de la corba en metres
g = acceleració de la gravetat terrestre. 9,81 m/s2
En una via peraltada, al costat del radi i el coeficient de fregament transversal caldrà tenir en compte la component de la força de gravetat a conseqüència del desnivell transversal de la via, per la qual cosa haurem d’introduir a la formulació el factor de correcció del coeficient de fregament.
Aquest factor pren el valor de la tangent de l’angle d’inclinació.
D’aquesta manera la velocitat crítica vindrà donada:
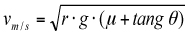
La formulació de dinàmica del vehicle exposada no considera l’acció dels sistemes de suspensió o ajuda el/la conductor/a mitjançant els moderns controls electrònics d’estabilitat, per la qual cosa el resultat obtingut serà inferior al real.
4.4.2. Radi d’una corba
El radi de la corba s’ha de tenir en compte per determinar la velocitat màxima a la qual un vehicle pot agafar-la sense que es produeixi el derrapatge.
Un mètode per a l’obtenció del radi consisteix a traçar la corda que uneix els dos extrems de la corba, es a dir, de l’arc de la circumferència, i posteriorment la sagita.

La relació entre el radi de la circumferència, la corda i la sagita, definits en metres, s’expressa matemàticament així:

4.5. Atropellaments
4.5.1. Conceptes fonamentals
Fase de l’atropellament
Es defineix l’atropellament com la presa de contacte més o menys violenta d’un vehicle amb un/a vianant.
López-Muñiz (1995) el divideix en diferents fases que poden arribar a produir-se després del contacte inicial entre el vehicle amb el/la vianant.
-
Caiguda. Es produeix quan a conseqüència de l’empenta la víctima és llançada pel vehicle a una distància més o menys gran.
-
Acostament. Es produeix quan el vehicle entra novament en contacte amb el cos caigut i l’aparta o sobrepassa.
-
Compressió. És el fet que passi almenys una roda per sobre del cos caigut.
-
Arrossegament. Abans o després de sobrepassar-la, la víctima és arrossegada pel vehicle durant una part del trajecte.
Variants en la projecció de la persona atropellada
Alguns estudis efectuats sobre la seqüència d’aquest tipus d’accidents han demostrat que els factors principals que influeixen de manera decisiva en la projecció de la persona atropellada són:

-
La velocitat del vehicle.
-
L’alçada del perfil frontal del vehicle.
-
L’alçada del centre de gravetat de la persona
En funció d’aquests paràmetres es poden definir unes variants cinemàtiques de la trajectòria postimpacte del cos de la persona atropellada:
-
Projecció (wrap trajectory).
-
Transport (forward proyection).
-
Volteig sobre el para-xocs (wrap).
-
Volteig sobre el sostre (roof vault).
Projecció (wrap trajectory)

En el primer moment de l’accident es produeix un contacte inicial entre la part frontal del vehicle i el/la vianant.
Si el centre de gravetat del vianant està a una alçada superior al perfil frontal del vehicle es genera un desequilibri i un moviment de caiguda del vianant sobre el vehicle.
Durant l’avançament del vehicle es produeix un segon contacte del vianant contra el capó i/o parabrisa, fase durant la qual adquireix momentàniament la seva velocitat.
Quan s’accionen els frens del vehicle (si no s’han accionat abans del contacte inicial), el cos del vianant és projectat traçant una trajectòria parabòlica a la velocitat que havia adquirit, l’estudi de la qual cosa ens permet efectuar un dictamen tècnic de la velocitat del vehicle a partir de models matemàtics.
Transport (forward projection)
Aquest tipus d’atropellament es distingeix perquè la part superior del frontal del vehicle està a una alçada superior o igual al centre de gravetat del vianant.
També es produeix quan un vehicle de frontal baix atropella un menor d’edat, ja que el centre de gravetat està a una alçada inferior a la del capó del vehicle.
Un cop produït el contacte inicial, en ser accionat el pedal del fre, el/la vianant és projectat/da en el sentit de la marxa del vehicle traçant una paràbola d’escassos graus respecte al sòl.
En cas que no es produeixi la reducció de velocitat del vehicle, o es demori, es produirà un transport del vianant, que al seu torn anirà caient a la calçada i podrà arribar a ser atropellat.
Volteig sobre el para-xocs (wrap)
Es produeix quan el cos del vianant és aconseguit per una de les zones exteriors del frontal del vehicle i és voltejat cap a l’exterior de la trajectòria del vehicle sense que s’arribi a produir un segon impacte.
Volteig sobre el sostre
Es caracteritza per una velocitat elevada del vehicle. Després del primer impacte, el/la vianant és voltejat/da sobre el sostre o part posterior del vehicle.
4.5.2. Mètode Searle
Són nombrosos els models matemàtics que tenen per objecte determinar la velocitat d’atropellament a partir de la distància de projecció de la persona atropellada.
El 1983, l’investigador John A. Searle va presentar una formulació amb la finalitat de fixar la velocitat en què es produeix l’atropellament.

El mètode presentat per Searle, adaptat a les circumstàncies reals dels atropellaments, estima l’alçada inicial de projecció de la persona i la fase posterior que comprèn el desplaçament del vianant des de la seva caiguda a la calçada fins a assolir la seva posició final, procés durant el qual es poden produir una sèrie de rebots, girs o lliscaments.
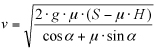
En què:
µ = coeficient de fregament del cos del vianant.
v = velocitat de projecció del cos del vianant, en m/s.
d = distància de projecció.
h = alçada de l’inici de projecció del vianant.
α = angle de projecció.
g = valor de l’acceleració de la gravetat.
Velocitat mínima
Com que l’angle de projecció de la persona és una variable desconeguda, una correcció a l’equació inicial permet a Searle obtenir la velocitat mínima a la qual està projectada, independentment de l’angle de llançament.
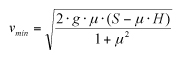
Uns experiments que Searle va dur a terme durant assajos amb dummies suggereixen que cal fer unes correccions a l’expressió inicial en virtut de les condicions en què es produeixi l’atropellament:
-
Coeficient de fregament del vianant.
-
Desnivell de la via.
-
Angle de projecció.
Correcció en funció del coeficient de fregament del vianant
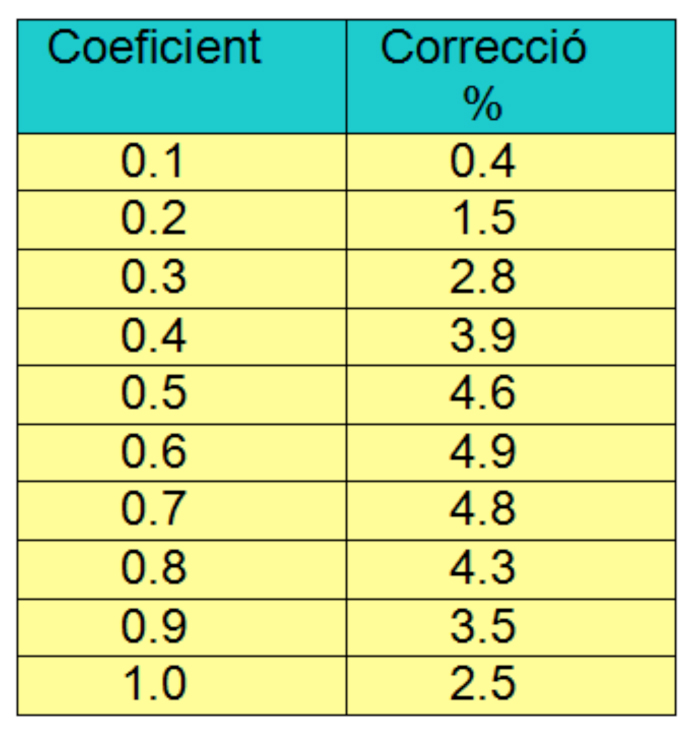
D’acord amb les dades exposades a la taula, a la velocitat de projecció obtinguda s’ha de deduir el percentatge que es relaciona directament amb l coeficient de fregament del seu cos.
| Pell (no rodant) | 0.6 – 0.7 |
| Polièster o altres sintètics (no rodant) | 0.7 |
| Cotó o llana (no rodant) | 0.7 – 0.9 |
| Qualsevol altre material rodant | 1.0 |
En un atropellament ocorregut en una calçada d’aglomerat asfàltic sec, en què la roba del vianant és de polièster o cotó, amb un coeficient de 0.7, haurem de corregir la velocitat obtinguda en l’expressió anterior i caldrà que restem el 4,8% del seu valor.
Eficàcia de projecció
Un cop coneguda la velocitat de projecció del vianant, s’ha de considerar que la velocitat a la qual és projectada la persona és més baixa que la velocitat de circulació del vehicle. Searle, basant-se en els assajos duts a terme, proposa les correccions següents:
| Velocitat del vehicle | |
| Persones adultes | Velocitat de projecció del vianant + 20% |
| Nens | Velocitat de projecció del vianant + 10% |