Anàlisi de problemes i presa de decisions
4. Estructura dels problemes de decisió
4.1. Elements d'un problema de decisió
En cada problema de decisió pots distingir una sèrie d'elements característics:
-
El decisor: Encarregat de triar la millor forma d'actuar d'acord amb els seus interessos. És el responsable de la decisió. Pot ser un individu o un grup d'individus. Suposadament és racional, consistent i coherent. Decideix com, amb qui i quines metodologies s'utilitzaran.
-
Alternatives o accions: Són les formes d'actuar possibles, les opcions que tens, de les quals has de seleccionar-ne una. Han de ser excloents entre si. Estan en competència. Has d'avaluar-les de forma homogènia i justa.
-
Possibles estats de la naturalesa: Amb aquest nom es designen tots aquells esdeveniments futurs que escapen al control del decisor i que influeixen en el procés, és a dir, tots els escenaris possibles. Concretament, són els futurs possibles. Corresponen a les accions de la naturalesa o d'altres grups de persones diferents del decisor i que no són controlades per ell.
-
Conseqüències o resultats de la decisió: S'obtenen en seleccionar les diferents alternatives segons cadascun dels possibles estats de la naturalesa. Són els beneficis o perjudicis de diferent naturalesa ocasionats en el futur per les decisions preses en el present.
-
Regla de decisió o criteri: És l'especificació d'un procediment per identificar la millor alternativa en un problema de decisió (objectius, atributs, metes). És tracta de la definició del que busques i com avalues el que busques, és a dir, les preferències del decisor, que és el que estableix els seus interessos i les seves importàncies relatives. Els models i regles de decisió no són decisors, són un suport per a l'anàlisi en la presa de decisió.
En tipus de decisions que no són aïllades, sinó seqüencials, de manera que les decisions es prenen de forma successiva i estan totes elles interrelacionades, s'utilitza, com a element de representació i anàlisi, la matriu de criteris o l'arbre de decisió.
4.2. Arbres de decisió
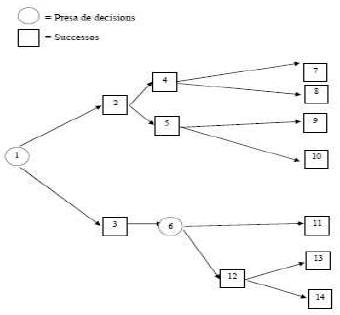
Un arbre de decisió ve a ser un camí que porta d'un vèrtex a un altre. Els símbols que s'utilitzen en la representació gràfica són:
-
Els vèrtexs o nusos: Representen un concepte de la realitat que s'està estudiant i se situen en un moment puntual. Hi ha dos tipus de vèrtexs o nusos:
-
Nusos de decisió: Simbolitzen l'instant en què el subjecte decisor/òra es veu obligat/ada a decidir entre diverses alternatives. Representen l'origen de diverses branques de decisió. Gràficament es representen com un cercle.
-
Nusos aleatoris: Representen els resultats possibles de cada elecció, de manera que de cada nus aleatori parteixen tantes branques com estats de la natura existeixin. Gràficament es representen com un quadrat.
-
-
Els arcs o branques: Són les eventualitats que es poden presentar a cada moment i es representen mitjançant una línia que uneix dos nusos consecutius. També hi ha dos tipus d'arcs o branques:
-
Branques de decisió: Parteixen de nusos de decisió i representen les alternatives que té davant seu el subjecte decisor/òra.
-
Branques aleatòries: Parteixen de nusos aleatoris i representen diferents estats de la natura.
-
Al final de tota la seqüència de decisions i estats de la natura, has de portar a terme les valoracions de cada seqüència de decisions i successos, expressades en unitats monetàries. Faràs aquestes valoracions al final de cada branca i es referiran al moment inicial (valor actual net).
El procés de construcció i resolució conté les fases següents:
-
Identificació del problema i de l’horitzó temporal.
-
Inici de l’arbre per un punt o nus de decisió.
-
Continuació del procés dibuixant els diferents nusos aleatoris o de decisió.
-
Assignació de les probabilitats a cada branca aleatòria.
-
Enumeració dels nusos de decisió i aleatoris.
-
Valoració de les terminacions de l’arbre. Per a això utilitzarem el valor actual net.
-
Resolució de l’arbre de decisió aplicant el mètode d’avançament cap a enrere, és a dir, en sentit invers a la seva construcció.
Cas exemple
Una empresa catalana de vi i cava vol vendre els seus productes als EUA. Té dues possibilitats:
-
Treure un tipus de cava, que primer es llançarà a Espanya, amb una probabilitat d’èxit del 65%. Si el producte fracassa a Espanya, l’empresari tindrà unes pèrdues de 75.000 €, i només si triomfa a Espanya, l’empresari es plantejarà anar als EUA, ja que els beneficis a Espanya (200.000 €) li permetran afrontar el mercat americà. Les probabilitats d’èxit als EUA són del 40%, de manera que els guanys serien de 400.000 €, i si fracassa, els beneficis totals seran de 100.000 €.
-
D’altra banda, pot llançar un producte als EUA que ja tingui èxit a Espanya (vi negre). Si es decideix per aquesta inversió, té un 50% de probabilitats d’èxit i de poder guanyar 350.000 €, encara que si fracassa, les seves pèrdues pujarien a 80.000 €.
Si hem d’assessorar l’empresa, fem primer un diagrama d’arbre:
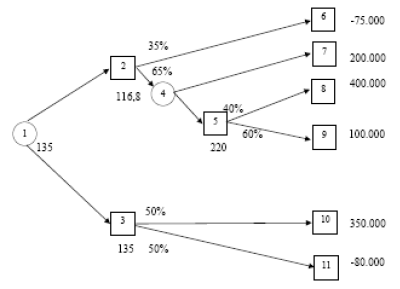
En segon lloc, calculem els resultats actualitzats de cada alternativa:
VAN (6) = -75.000
VAN (7) = 200.000
VAN (8) = 400.000
VAN (9) = 100.000
VAN (10) = 350.000
VAN (11) = -80.000
En tercer lloc, calculem els valors dels altres nusos per poder prendre una decisió.
VE(5) = (100.000 * 0,60) + (400.000 * 0,40) = 220.000
VE(4) = 220.000 (el més gran esperat)
VE(2) = (-75.000 * 0,35) + (220.000 * 0,65) = 116.750
VE(3) = (-80.000 * 0,50) + (350.000 * 0,50) = 135.000
VE(1) = 135.000 (el més gran esperat)
Per tant, invertirem en vi negre als EUA.