L’anàlisi de dades és el procediment o procés que es realitza per organitzar i extreure la informació recollida pels investigadors. En aquest procediment s’estableixen relacions, interpretacions i significats de les dades obtingudes.
Abans d’analitzar les dades, és convenient conèixer quin és el seu abast i sobre què estan parlant. Per això és important tenir en compte els conceptes d’univers/població, cens i mostra.
-
L’univers o població és el conjunt total d’individus (persones, objectes, centres escolars, associacions…) sobre els quals es vol realitzar un estudi o una anàlisi.
-
Un cens és un llistat complet de totes les persones que formen part d’una població o un univers determinats.
-
Una mostra és una part de l’univers o la població que es vol estudiar, sobre la qual s’observa determinades característiques que després es voldran extrapolar o inferir a la població o l’univers en general.
Normalment es treballa sobre mostres perquè d’aquesta manera s’abarateixen els costos que suposa haver d’arribar a tota la població. Però llavors s’ha de tenir en compte que és possible caure en els errors mostrals, és a dir, mesures esbiaixades sobre la població o l’univers perquè existeix un biaix en la mostra.
El càlcul de la mida de la mostra (grandària mostral) i de l’error mostral acceptable en la mostra es poden calcular.
La mostra pot ser:
-
Probabilística: mostra en què el conjunt d’individus de la població té la mateixa probabilitat de ser seleccionat per formar part de la mostra, és a dir, que se selecciona de forma aleatòria.
-
No probabilística: mostra que s’escull de forma intencionada.
Dintre de les mostres probabilístiques, existeixen diversos tipus de mostreig:
-
Probabilístic
-
Aleatori simple
-
Sistemàtic
-
Estratificat
-
Per conglomerats
-
Polietàpic
-
-
No probabilístic
-
Per quotes
-
Casual o incidental
-
De conveniència
-
Intencional o raonat
-
Bola de neu
-
Exemples de població o univers:
-
Alumnat d’un centre educatiu
-
Famílies residents en un barri o municipi
-
Escoles en un municipi
-
Joves participants en el projecte que s’avalua
-
…
L’aleatorietat no implica atzar. Per seleccionar una mostra sobre un univers del qual es disposa d’un cens, una opció és utilitzar la mostra sistemàtica. Consisteix a ordenar el cens i enumerar-lo, calcular un període (nombre total d’individus a la població / nombre total d’individus al cens) i seleccionar les unitats mostrals que coincideixin amb aquest període.
En cas que sigui assumible analitzar l’univers complet, ja sigui perquè és reduït o perquè es té «captiu», sempre és preferible. De totes maneres, s’ha de tenir en compte un altre tipus d’error, el sistemàtic, que pot produir-se per la no obtenció d’informació dels individus o per un error en la mesura.
Aquesta és la primera anàlisi que s’acostuma a fer de les dades. Amb dades de tipus qualitatiu, l’anàlisi es fa mitjançant una taula de freqüències.
Les taules de freqüències es fan calculant quantes vegades ocorre cadascuna de les possibles opcions d’una variable. A més, es calcula quant representa aquesta freqüència sobre, en termes percentuals, el total d’informació.
Taula de freqüències dels alumnes del cicle
| Freqüència | Percentatge | |
| Cicle inicial | 250 | 27,59 % |
| Cicle mitjà | 325 | 35,87 % |
| Cicle superior | 331 | 36,53 % |
| Total | 906 | 100 % |
Amb les dades numèriques, com els indicadors, es fan servir mesures de tendència central i de dispersió.
Les mesures de tendència central més utilitzades són:
-
Moda: és el valor que es repeteix més vegades.
-
Mediana: és el valor que, endreçats tots els valors per ordre, queda al mig (deixa el 50 % dels valors a esquerra i dreta).
-
Mitjana aritmètica: és la suma de tots els valors disponibles dividida entre el nombre d’individus.
La mesura de dispersió més utilitzada és la desviació estàndard, que informa sobre si la distribució de les dades està molt concentrada al voltant de la mitjana (quan representa valors baixos) o està més dispersa (valors elevats).
També és molt útil la utilització dels quartils, sobretot el segon i tercer quartils, que mostren, respectivament, quin és el valor que queda a l’esquerra i a la dreta el 25 % dels casos. Per calcular-los és necessari, tal com es feia també amb la mediana, ordenar els valors obtinguts i identificar quins són els dos valors que compleixen la característica mencionada.
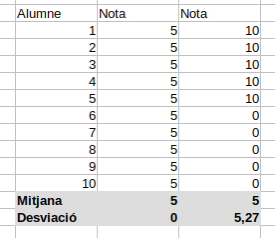
Aquests càlculs es poden fer normalment amb els fulls de càlcul o el programari d’anàlisi estadística. És important poder donar una visió conjunta de la distribució de les dades, ja que no és el mateix, en una aula d’alumnes que tenen de mitjana un 5, que aquesta mitjana sigui perquè tots han tret un 5 que perquè n’hi ha 5 que han tret un 10 i 5 que han tret un zero.
Per aclarir l’exemple esmentat, que deia que no és el mateix, en una aula d’alumnes que tenen de mitjana un 5, que aquesta mitjana sigui perquè tots han tret un 5 que perquè n’hi ha 5 que han tret un 10 i 5 que han tret un zero, la taula següent mostra les diferències:
